Difference between pages "Decreasing sequence" and "Dirac monopole"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | A | + | A solution to the [[Maxwell equations|Maxwell equations]] describing a point source of a [[Magnetic field|magnetic field]]. In 1931, P.A.M. Dirac [[#References|[a1]]] considered the quantum mechanics of the electron in a magnetic field (due to a point source), |
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301301.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301302.png" /> is the length of the position vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301303.png" /> in the Cartesian coordinates and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301304.png" /> is a constant determining the strength of the field, known as a magnetic charge of the monopole. Since the induction vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301305.png" /> in (a1) is central, it can be conveniently written in the [[Spherical coordinates|spherical coordinates]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301306.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301307.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301308.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d1301309.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013011.png" />. In these coordinates, only the radial component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013012.png" /> is non-zero and equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013013.png" />. Maxwell's equations imply that there is no single vector potential corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013014.png" /> defined on the whole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013015.png" />. However, Dirac found that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013016.png" />, with vector potentials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013017.png" /> whose only non-zero components are in the azimuthal direction and read | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013018.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a2)</td></tr></table> | ||
| + | |||
| + | The potentials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013019.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013020.png" /> are singular at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013021.png" /> (the negative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013022.png" />-axis) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013023.png" /> (the positive <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013024.png" />-axis), respectively. These singularities are known as Dirac's string singularities. The union of the regions in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013025.png" /> are well-defined covers the whole of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013026.png" />. In the intersection of these regions (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013027.png" />) the vector potentials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013028.png" /> are related by the [[Gauge transformation|gauge transformation]], <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013029.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013030.png" />. If there is an electron in the magnetic field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013031.png" />, then in the region where both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013033.png" /> are well-defined, the wave functions of the electron corresponding to different vector potentials should be related by the gauge transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013034.png" />, i.e., | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013035.png" /></td> </tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013036.png" /> is the electric charge of the electron and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013037.png" /> is the [[Planck constant|Planck constant]] divided by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013038.png" />. The wave function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013039.png" /> is single valued if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013040.png" /> for an integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013041.png" />, i.e. if and only if the magnetic charge attains discrete values | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013042.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a3)</td></tr></table> | ||
| + | |||
| + | Thus, the consistency of the monopole field (a1) with quantum mechanics can be achieved, provided the magnetic charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013043.png" /> be quantized. Equation (a3) expresses also "duality" (reciprocity) between magnetic and electric charges: If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013045.png" /> are interchanged, (a3) remains the same. Dirac used this fact to explain the observed quantization of the electric charge: Should a magnetic monopole of charge, say, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013046.png" /> exist, then by the above argument the electric charge would be allowed to have only discrete values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013047.png" />. This argument, however, would leave the quantization of magnetic charge unexplained, a fact that Dirac found disappointing [[#References|[a1]]]. | ||
| + | |||
| + | In 1975, T.T. Wu and C.N. Yang [[#References|[a9]]] observed that Dirac's monopole of magnetic charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013048.png" /> has a natural topological interpretation as a [[Connection|connection]] in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013049.png" /> principal bundle over the two-sphere <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013050.png" /> with the first Chern number (the winding number) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013051.png" /> (cf. [[Connections on a manifold|Connections on a manifold]]; [[Principal fibre bundle|Principal fibre bundle]]; or [[#References|[a3]]] for a review). In natural units <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013052.png" />, the potentials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013053.png" /> can be written as one-forms | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013054.png" /></td> </tr></table> | ||
| + | |||
| + | and they are a connection one-form written in two charts covering <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013055.png" />. More precisely, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013056.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013057.png" /> above are coordinates of the two-sphere. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013058.png" /> is the north pole and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013059.png" /> is well-defined everywhere outside the north pole, for example on a chart <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013060.png" /> covering the southern hemisphere including the equator (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013061.png" />). On the other hand, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013062.png" /> is the south pole, and thus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013063.png" /> is well-defined everywhere except the south pole, for example on a chart <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013064.png" /> covering the northern hemisphere including the equator (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013065.png" />). The intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013066.png" /> is parametrized by the azimuthal angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013067.png" />. In order to combine this local system into a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013068.png" />-principal bundle, on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013069.png" /> the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013070.png" />-coordinate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013071.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013072.png" /> must be related to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013073.png" />-coordinate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013074.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013075.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013076.png" />, with integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013077.png" />. This explains the appearance of Dirac's string singularity when the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013078.png" /> are extended to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013079.png" />, and the fact that it can be removed by a gauge transformation which requires Dirac's quantization condition. Thus, the trivial bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013080.png" /> admits no monopole (charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013081.png" />-monopole). The existence of a monopole indicates non-triviality of a corresponding principal bundle. The monopole of charge <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013082.png" /> is the connection in the [[Hopf fibration|Hopf fibration]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013083.png" />, while the monopole of charge with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013084.png" /> corresponds to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013085.png" />-bundle over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013086.png" /> with the [[Lens space|lens space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013087.png" /> as a total space (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013088.png" /> is viewed inside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013089.png" /> as a subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013090.png" />th roots of the unit matrix) [[#References|[a7]]]. | ||
| + | |||
| + | The Dirac monopole is an example of an Abelian monopole, i.e., a solution of field equations of gauge theory with Abelian gauge group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013091.png" />. Since the mid-1970{}s there has been a considerable interest in non-Abelian monopoles, in particular those related to the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013093.png" /> gauge theories. In pure mathematics this was triggered in particular by the appearance of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013094.png" /> gauge theory in the classification of four-manifolds by S.K. Donaldson [[#References|[a2]]]. However, in 1994, E. Witten [[#References|[a8]]] showed that certain Abelian monopole equations motivated by the supersymmetric quantum field theory [[#References|[a5]]], [[#References|[a6]]] and known as the Seiberg–Witten equations, can be used to derive both the Donaldson invariants of four-manifolds as well as new ones (the Seiberg–Witten invariants; cf. also [[Four-dimensional manifold|Four-dimensional manifold]]). It was soon noted [[#References|[a4]]] that the Dirac gauge potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013095.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013096.png" /> provides a bosonic part of the simplest (not <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013097.png" />) solution to Seiberg–Witten equations. Witten's observation, as well as the appearance of magnetic monopoles in string theory, revived the interest in both monopoles and the reciprocity between electric and magnetic charges (electric-magnetic duality). | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A.M. Dirac, "Quantized singularities in the electromagnetic field" ''Proc. Royal Soc. London'' , '''A133''' (1931) pp. 60–72</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.K. Donaldson, P.B. Kronheimer, "The geometry of four-manifolds" , Clarendon Press/Oxford Univ. Press (1990) {{MR|1079726}} {{ZBL|0820.57002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Eguchi, P.B. Gilkey, A.J. Hanson, "Gravitation, gauge theories and differential geometry" ''Phys. Rept.'' , '''66''' : 6 (1980) pp. 213–393 {{MR|0598586}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> P.G.O. Freund, "Dirac monopoles and the Seiberg–Witten monopole equations" ''J. Math. Phys.'' , '''36''' (1995) pp. 2673–2674 {{MR|1331281}} {{ZBL|0845.58070}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> N. Seiberg, E. Witten, "Electric-magnetic duality: monopole condensation, and confinement in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013098.png" /> supersymmetric Yang–Mills theory" ''Nucl. Phys.'' , '''B426''' (1994) pp. 19–52 {{MR|}} {{ZBL|0996.81511}} {{ZBL|0996.81510}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> N. Seiberg, E. Witten, "Monopoles, duality and chiral symmetry breaking in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d130/d130130/d13013099.png" /> supersymmetric QCD" ''Nucl. Phys.'' , '''B431''' (1994) pp. 484–550 {{MR|1306869}} {{ZBL|1020.81911}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Trautman, "Solutions of Maxwell and Yang–Mills equations associated with Hopf fiberings" ''Internat. J. Theoret. Phys.'' , '''16''' (1977) pp. 561–565</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E. Witten, "Monopoles and four-manifolds" ''Math. Res. Lett.'' , '''1''' (1994) pp. 769–796 {{MR|1306021}} {{ZBL|0867.57029}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> T.T. Wu, C.N. Yang, "Concept of nonintegrable phase factors and global formulation of gauge fields" ''Phys. Rev.'' , '''D12''' (1975) pp. 3845–3857 {{MR|0426712}} {{ZBL|}} </TD></TR></table> | ||
Revision as of 16:56, 15 April 2012
A solution to the Maxwell equations describing a point source of a magnetic field. In 1931, P.A.M. Dirac [a1] considered the quantum mechanics of the electron in a magnetic field (due to a point source),
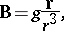 | (a1) |
where 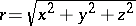 is the length of the position vector
is the length of the position vector 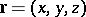 in the Cartesian coordinates and
in the Cartesian coordinates and 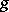 is a constant determining the strength of the field, known as a magnetic charge of the monopole. Since the induction vector
is a constant determining the strength of the field, known as a magnetic charge of the monopole. Since the induction vector 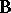 in (a1) is central, it can be conveniently written in the spherical coordinates
in (a1) is central, it can be conveniently written in the spherical coordinates 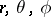 defined by
defined by 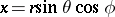 ,
, 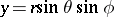 ,
, 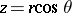 ,
, 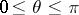 ,
, 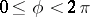 . In these coordinates, only the radial component of
. In these coordinates, only the radial component of 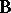 is non-zero and equals
is non-zero and equals 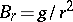 . Maxwell's equations imply that there is no single vector potential corresponding to
. Maxwell's equations imply that there is no single vector potential corresponding to 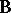 defined on the whole of
defined on the whole of 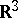 . However, Dirac found that
. However, Dirac found that 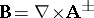 , with vector potentials
, with vector potentials 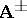 whose only non-zero components are in the azimuthal direction and read
whose only non-zero components are in the azimuthal direction and read
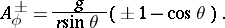 | (a2) |
The potentials 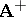 ,
, 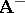 are singular at
are singular at 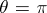 (the negative
(the negative  -axis) and
-axis) and 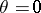 (the positive
(the positive  -axis), respectively. These singularities are known as Dirac's string singularities. The union of the regions in which
-axis), respectively. These singularities are known as Dirac's string singularities. The union of the regions in which 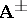 are well-defined covers the whole of
are well-defined covers the whole of 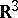 . In the intersection of these regions (
. In the intersection of these regions ( ) the vector potentials
) the vector potentials 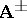 are related by the gauge transformation,
are related by the gauge transformation, 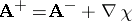 , with
, with 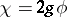 . If there is an electron in the magnetic field
. If there is an electron in the magnetic field 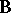 , then in the region where both
, then in the region where both 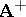 and
and 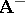 are well-defined, the wave functions of the electron corresponding to different vector potentials should be related by the gauge transformation
are well-defined, the wave functions of the electron corresponding to different vector potentials should be related by the gauge transformation 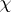 , i.e.,
, i.e.,
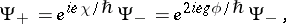 |
where  is the electric charge of the electron and
is the electric charge of the electron and 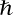 is the Planck constant divided by
is the Planck constant divided by 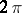 . The wave function
. The wave function 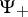 is single valued if and only if
is single valued if and only if 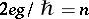 for an integer
for an integer  , i.e. if and only if the magnetic charge attains discrete values
, i.e. if and only if the magnetic charge attains discrete values
 | (a3) |
Thus, the consistency of the monopole field (a1) with quantum mechanics can be achieved, provided the magnetic charge 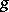 be quantized. Equation (a3) expresses also "duality" (reciprocity) between magnetic and electric charges: If
be quantized. Equation (a3) expresses also "duality" (reciprocity) between magnetic and electric charges: If 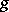 and
and  are interchanged, (a3) remains the same. Dirac used this fact to explain the observed quantization of the electric charge: Should a magnetic monopole of charge, say,
are interchanged, (a3) remains the same. Dirac used this fact to explain the observed quantization of the electric charge: Should a magnetic monopole of charge, say, 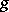 exist, then by the above argument the electric charge would be allowed to have only discrete values
exist, then by the above argument the electric charge would be allowed to have only discrete values 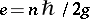 . This argument, however, would leave the quantization of magnetic charge unexplained, a fact that Dirac found disappointing [a1].
. This argument, however, would leave the quantization of magnetic charge unexplained, a fact that Dirac found disappointing [a1].
In 1975, T.T. Wu and C.N. Yang [a9] observed that Dirac's monopole of magnetic charge 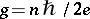 has a natural topological interpretation as a connection in the
has a natural topological interpretation as a connection in the 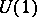 principal bundle over the two-sphere
principal bundle over the two-sphere 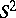 with the first Chern number (the winding number)
with the first Chern number (the winding number) 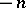 (cf. Connections on a manifold; Principal fibre bundle; or [a3] for a review). In natural units
(cf. Connections on a manifold; Principal fibre bundle; or [a3] for a review). In natural units 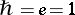 , the potentials
, the potentials 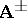 can be written as one-forms
can be written as one-forms
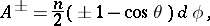 |
and they are a connection one-form written in two charts covering 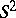 . More precisely,
. More precisely, 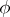 ,
, 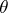 above are coordinates of the two-sphere. Then
above are coordinates of the two-sphere. Then 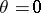 is the north pole and
is the north pole and 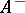 is well-defined everywhere outside the north pole, for example on a chart
is well-defined everywhere outside the north pole, for example on a chart 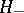 covering the southern hemisphere including the equator (
covering the southern hemisphere including the equator (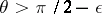 ). On the other hand,
). On the other hand, 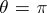 is the south pole, and thus
is the south pole, and thus 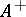 is well-defined everywhere except the south pole, for example on a chart
is well-defined everywhere except the south pole, for example on a chart 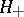 covering the northern hemisphere including the equator (
covering the northern hemisphere including the equator (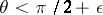 ). The intersection
). The intersection 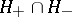 is parametrized by the azimuthal angle
is parametrized by the azimuthal angle 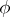 . In order to combine this local system into a
. In order to combine this local system into a 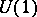 -principal bundle, on
-principal bundle, on 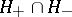 the
the 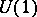 -coordinate
-coordinate 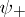 over
over 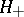 must be related to the
must be related to the 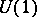 -coordinate
-coordinate 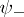 over
over 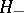 by
by  , with integer
, with integer  . This explains the appearance of Dirac's string singularity when the
. This explains the appearance of Dirac's string singularity when the 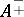 are extended to
are extended to 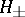 , and the fact that it can be removed by a gauge transformation which requires Dirac's quantization condition. Thus, the trivial bundle
, and the fact that it can be removed by a gauge transformation which requires Dirac's quantization condition. Thus, the trivial bundle 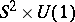 admits no monopole (charge
admits no monopole (charge  -monopole). The existence of a monopole indicates non-triviality of a corresponding principal bundle. The monopole of charge
-monopole). The existence of a monopole indicates non-triviality of a corresponding principal bundle. The monopole of charge 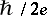 is the connection in the Hopf fibration
is the connection in the Hopf fibration 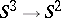 , while the monopole of charge with
, while the monopole of charge with 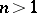 corresponds to the
corresponds to the 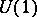 -bundle over
-bundle over 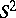 with the lens space
with the lens space 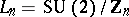 as a total space (
as a total space (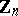 is viewed inside
is viewed inside 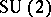 as a subgroup of
as a subgroup of  th roots of the unit matrix) [a7].
th roots of the unit matrix) [a7].
The Dirac monopole is an example of an Abelian monopole, i.e., a solution of field equations of gauge theory with Abelian gauge group 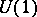 . Since the mid-1970{}s there has been a considerable interest in non-Abelian monopoles, in particular those related to the
. Since the mid-1970{}s there has been a considerable interest in non-Abelian monopoles, in particular those related to the 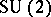 gauge theories. In pure mathematics this was triggered in particular by the appearance of
gauge theories. In pure mathematics this was triggered in particular by the appearance of 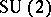 gauge theory in the classification of four-manifolds by S.K. Donaldson [a2]. However, in 1994, E. Witten [a8] showed that certain Abelian monopole equations motivated by the supersymmetric quantum field theory [a5], [a6] and known as the Seiberg–Witten equations, can be used to derive both the Donaldson invariants of four-manifolds as well as new ones (the Seiberg–Witten invariants; cf. also Four-dimensional manifold). It was soon noted [a4] that the Dirac gauge potential
gauge theory in the classification of four-manifolds by S.K. Donaldson [a2]. However, in 1994, E. Witten [a8] showed that certain Abelian monopole equations motivated by the supersymmetric quantum field theory [a5], [a6] and known as the Seiberg–Witten equations, can be used to derive both the Donaldson invariants of four-manifolds as well as new ones (the Seiberg–Witten invariants; cf. also Four-dimensional manifold). It was soon noted [a4] that the Dirac gauge potential 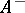 with
with 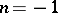 provides a bosonic part of the simplest (not
provides a bosonic part of the simplest (not  ) solution to Seiberg–Witten equations. Witten's observation, as well as the appearance of magnetic monopoles in string theory, revived the interest in both monopoles and the reciprocity between electric and magnetic charges (electric-magnetic duality).
) solution to Seiberg–Witten equations. Witten's observation, as well as the appearance of magnetic monopoles in string theory, revived the interest in both monopoles and the reciprocity between electric and magnetic charges (electric-magnetic duality).
References
| [a1] | P.A.M. Dirac, "Quantized singularities in the electromagnetic field" Proc. Royal Soc. London , A133 (1931) pp. 60–72 |
| [a2] | S.K. Donaldson, P.B. Kronheimer, "The geometry of four-manifolds" , Clarendon Press/Oxford Univ. Press (1990) MR1079726 Zbl 0820.57002 |
| [a3] | T. Eguchi, P.B. Gilkey, A.J. Hanson, "Gravitation, gauge theories and differential geometry" Phys. Rept. , 66 : 6 (1980) pp. 213–393 MR0598586 |
| [a4] | P.G.O. Freund, "Dirac monopoles and the Seiberg–Witten monopole equations" J. Math. Phys. , 36 (1995) pp. 2673–2674 MR1331281 Zbl 0845.58070 |
| [a5] | N. Seiberg, E. Witten, "Electric-magnetic duality: monopole condensation, and confinement in 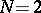 supersymmetric Yang–Mills theory" Nucl. Phys. , B426 (1994) pp. 19–52 Zbl 0996.81511 Zbl 0996.81510 supersymmetric Yang–Mills theory" Nucl. Phys. , B426 (1994) pp. 19–52 Zbl 0996.81511 Zbl 0996.81510 |
| [a6] | N. Seiberg, E. Witten, "Monopoles, duality and chiral symmetry breaking in 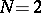 supersymmetric QCD" Nucl. Phys. , B431 (1994) pp. 484–550 MR1306869 Zbl 1020.81911 supersymmetric QCD" Nucl. Phys. , B431 (1994) pp. 484–550 MR1306869 Zbl 1020.81911 |
| [a7] | A. Trautman, "Solutions of Maxwell and Yang–Mills equations associated with Hopf fiberings" Internat. J. Theoret. Phys. , 16 (1977) pp. 561–565 |
| [a8] | E. Witten, "Monopoles and four-manifolds" Math. Res. Lett. , 1 (1994) pp. 769–796 MR1306021 Zbl 0867.57029 |
| [a9] | T.T. Wu, C.N. Yang, "Concept of nonintegrable phase factors and global formulation of gauge fields" Phys. Rev. , D12 (1975) pp. 3845–3857 MR0426712 |
Decreasing sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Decreasing_sequence&oldid=13355