Difference between pages "Multi-valued representation" and "Vector bundle"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | + | A [[Fibre space|fibre space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963801.png" /> each fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963802.png" /> of which is endowed with the structure of a (finite-dimensional) [[Vector space|vector space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963803.png" /> over a skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963804.png" /> such that the following local triviality condition is satisfied. Each point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963805.png" /> has an open neighbourhood <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963806.png" /> and an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963807.png" />-isomorphism of fibre bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963808.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v0963809.png" /> is an isomorphism of vector spaces for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638010.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638011.png" /> is said to be the dimension of the vector bundle. The sections of a vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638012.png" /> form a locally free module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638013.png" /> over the ring of continuous functions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638014.png" /> with values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638015.png" />. A morphism of vector bundles is a morphism of fibre bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638016.png" /> for which the restriction to each fibre is linear. The set of vector bundles and their morphisms forms the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638017.png" />. The concept of a vector bundle arose as an extension of the [[Tangent bundle|tangent bundle]] and the [[Normal bundle|normal bundle]] in differential geometry; by now it has become a basic tool for studies in various branches of mathematics: differential and algebraic topology, the theory of linear connections, algebraic geometry, the theory of (pseudo-) differential operators, etc. | |
| − | + | A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638018.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638019.png" /> is a vector bundle and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638020.png" /> is a vector subspace in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638021.png" /> is said to be a subbundle of the vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638022.png" />. For instance, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638023.png" /> be a vector space and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638024.png" /> be the [[Grassmann manifold|Grassmann manifold]] of subspaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638025.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638026.png" />; the subspace of the product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638027.png" />, consisting of pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638028.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638029.png" />, will then be a subbundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638030.png" /> of the trivial vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638031.png" />. The union of all vector spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638032.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638033.png" /> is a subbundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638034.png" /> endowed with the quotient topology, is said to be a quotient bundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638035.png" />. Let, furthermore, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638036.png" /> be a vector space and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638037.png" /> be the Grassmann manifold of subspaces of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638038.png" /> of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638039.png" />; the quotient bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638040.png" /> of the trivial vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638041.png" /> is defined as the quotient space of the product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638042.png" /> by the subbundle consisting of all pairs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638043.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638044.png" />. The concepts of a subbundle and a quotient bundle are used in contraction and glueing operations used to construct vector bundles over quotient spaces. | |
| + | |||
| + | A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638045.png" />-morphism of vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638046.png" /> is said to be of constant rank (pure) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638047.png" /> is locally constant on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638048.png" />. Injective and surjective morphisms are exact and are said to be monomorphisms and epimorphisms of the vector bundle, respectively. The following vector bundles are uniquely defined for a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638049.png" /> of locally constant rank: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638050.png" /> (the kernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638051.png" />), which is a subbundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638052.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638053.png" /> (the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638054.png" />), which is a subbundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638055.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638056.png" /> (the cokernel of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638057.png" />), which is a quotient bundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638058.png" />; and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638059.png" /> (the co-image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638060.png" />), which is a quotient bundle of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638061.png" />. Any subbundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638062.png" /> is the image of some monomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638063.png" />, while any quotient bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638064.png" /> is the cokernel of some epimorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638065.png" />. A sequence of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638066.png" />-morphisms of vector bundles | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638067.png" /></td> </tr></table> | ||
| + | |||
| + | is said to be exact if the sequence | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638068.png" /></td> </tr></table> | ||
| + | |||
| + | is exact for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638069.png" />. In particular, the sequence | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638070.png" /></td> </tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638071.png" /> is the zero vector bundle, is exact if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638072.png" /> is a monomorphism, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638073.png" /> is an epimorphism and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638074.png" />. The set of vector bundles over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638075.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638076.png" />-morphisms of locally constant rank forms an exact subcategory <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638077.png" /> of the category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638078.png" />. | ||
| + | |||
| + | For any vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638079.png" /> and mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638080.png" />, the [[Induced fibre bundle|induced fibre bundle]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638081.png" /> is endowed with a vector bundle structure such that the morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638082.png" /> is a vector bundle morphism. This structure is unique and has the following property: Every fibre mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638083.png" /> is an isomorphism of vector spaces. For instance, a vector bundle of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638084.png" /> over a paracompact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638085.png" /> is isomorphic to one of the vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638087.png" /> induced by certain mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638088.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638089.png" />, respectively; moreover, homotopic mappings induce isomorphic vector bundles and, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638090.png" />, the converse is true: To isomorphic vector bundles there correspond homotopic mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638091.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638092.png" />. This is one of the fundamental theorems in the homotopic classification of vector bundles, expressing the universal character of the vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638093.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638094.png" /> with respect to the classifying mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638095.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638096.png" />. | ||
| + | |||
| + | Any continuous operation ([[Functor|functor]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638097.png" /> on the category of vector spaces uniquely determines a continuous functor on the category of vector bundles over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638098.png" />; in this way it is possible to construct bundles associated with a given vector bundle: tensor bundles, vector bundles of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v09638099.png" /> and, in particular, the dual vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380100.png" />, exterior powers of vector bundles, etc., whose sections are vector bundles with supplementary structures. These are extensively employed in practical applications. | ||
| + | |||
| + | A direct sum (Whitney sum) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380101.png" /> and tensor product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380102.png" /> have been defined for two vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380103.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380104.png" />. With respect to these operations the set of classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380105.png" /> of isomorphic vector bundles over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380106.png" /> forms a semi-ring which plays an important part in the construction of a [[K-functor|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380107.png" />-functor]]; thus, if for vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380108.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380109.png" /> there exist trivial vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380110.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380111.png" /> such that the vector bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380112.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380113.png" /> are isomorphic (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380114.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380115.png" /> are stably equivalent), then their images in the "completion" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380116.png" /> of the semi-ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380117.png" /> are identical; moreover, the fact that the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380118.png" /> and the set of classes of stably-equivalent vector bundles coincide follows from the existence of an inverse vector bundle for any vector bundle over a paracompact space. | ||
| + | |||
| + | For any vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380119.png" /> over a paracompact space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380120.png" /> there exists a section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380121.png" /> of the vector bundle | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380122.png" /></td> </tr></table> | ||
| + | |||
| + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380123.png" /> is a trivial one-dimensional vector bundle, which on each fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380124.png" /> is a positive-definite form, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380125.png" /> is metrizable; this makes it possible to establish, in particular, the splittability of an arbitrary exact sequence of vector bundles | ||
| + | |||
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380126.png" /></td> </tr></table> | ||
| + | |||
| + | in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380127.png" /> is metrizable, that is, the existence of a morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380128.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380129.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380130.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380131.png" /> is the imbedding into the first term and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380132.png" /> is the projection onto the second term. | ||
| + | |||
| + | If, in each fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380133.png" /> of the vector bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380134.png" />, one identifies the points lying on the same line passing through zero, one obtains a bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380135.png" />, which is associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380136.png" /> and is said to be its projectivization; a fibre of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380137.png" /> is the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380138.png" /> which is associated with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380139.png" />. This bundle is used to study Thom spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380140.png" /> (cf. [[Thom space|Thom space]]), used in the homotopic interpretation of classes of bordant manifolds, characteristic classes of vector bundles describing the homological properties of manifolds, etc. | ||
| + | |||
| + | The concept of a vector bundle can be generalized to the case when the fibre is an infinite-dimensional vector space; in doing so, one must distinguish between the different topologies of the space of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380141.png" />, suitably modify the definitions of a pure morphism and an exact sequence of morphisms, and also the construction of vector bundles associated with continuous functors on the category of infinite-dimensional vector spaces. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) {{MR|0242081}} {{ZBL|0653.53001}} {{ZBL|0284.53018}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380142.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III {{MR|1931083}} {{MR|1532744}} {{MR|0155257}} {{ZBL|1008.57001}} {{ZBL|0103.15101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) {{MR|0533884}} {{ZBL|0444.32004}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) {{MR|1335917}} {{MR|0202713}} {{ZBL|0376.14001}} </TD></TR></table> | ||
| + | |||
| + | |||
| + | |||
| + | ====Comments==== | ||
| + | For more on the universality and classifying properties of the bundles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380143.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380144.png" /> cf. [[Classifying space|Classifying space]] or [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[ | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) {{MR|0440554}} {{ZBL|0298.57008}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A fibre space 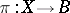 each fibre
each fibre 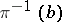 of which is endowed with the structure of a (finite-dimensional) vector space
of which is endowed with the structure of a (finite-dimensional) vector space 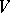 over a skew-field
over a skew-field 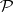 such that the following local triviality condition is satisfied. Each point
such that the following local triviality condition is satisfied. Each point 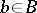 has an open neighbourhood
has an open neighbourhood 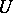 and an
and an  -isomorphism of fibre bundles
-isomorphism of fibre bundles 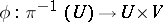 such that
such that 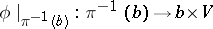 is an isomorphism of vector spaces for each
is an isomorphism of vector spaces for each 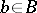 ;
; 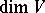 is said to be the dimension of the vector bundle. The sections of a vector bundle
is said to be the dimension of the vector bundle. The sections of a vector bundle 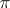 form a locally free module
form a locally free module 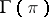 over the ring of continuous functions on
over the ring of continuous functions on 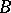 with values in
with values in 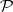 . A morphism of vector bundles is a morphism of fibre bundles
. A morphism of vector bundles is a morphism of fibre bundles 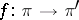 for which the restriction to each fibre is linear. The set of vector bundles and their morphisms forms the category
for which the restriction to each fibre is linear. The set of vector bundles and their morphisms forms the category  . The concept of a vector bundle arose as an extension of the tangent bundle and the normal bundle in differential geometry; by now it has become a basic tool for studies in various branches of mathematics: differential and algebraic topology, the theory of linear connections, algebraic geometry, the theory of (pseudo-) differential operators, etc.
. The concept of a vector bundle arose as an extension of the tangent bundle and the normal bundle in differential geometry; by now it has become a basic tool for studies in various branches of mathematics: differential and algebraic topology, the theory of linear connections, algebraic geometry, the theory of (pseudo-) differential operators, etc.
A subset 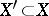 such that
such that 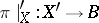 is a vector bundle and
is a vector bundle and 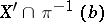 is a vector subspace in
is a vector subspace in 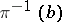 is said to be a subbundle of the vector bundle
is said to be a subbundle of the vector bundle 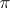 . For instance, let
. For instance, let 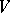 be a vector space and let
be a vector space and let  be the Grassmann manifold of subspaces of
be the Grassmann manifold of subspaces of  of dimension
of dimension 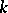 ; the subspace of the product
; the subspace of the product 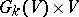 , consisting of pairs
, consisting of pairs 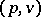 such that
such that  , will then be a subbundle
, will then be a subbundle 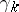 of the trivial vector bundle
of the trivial vector bundle 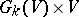 . The union of all vector spaces
. The union of all vector spaces 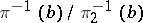 , where
, where 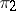 is a subbundle of
is a subbundle of 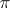 endowed with the quotient topology, is said to be a quotient bundle of
endowed with the quotient topology, is said to be a quotient bundle of 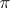 . Let, furthermore,
. Let, furthermore, 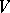 be a vector space and let
be a vector space and let 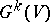 be the Grassmann manifold of subspaces of
be the Grassmann manifold of subspaces of 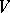 of codimension
of codimension 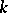 ; the quotient bundle
; the quotient bundle 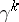 of the trivial vector bundle
of the trivial vector bundle 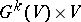 is defined as the quotient space of the product
is defined as the quotient space of the product 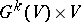 by the subbundle consisting of all pairs
by the subbundle consisting of all pairs 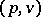 ,
, 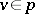 . The concepts of a subbundle and a quotient bundle are used in contraction and glueing operations used to construct vector bundles over quotient spaces.
. The concepts of a subbundle and a quotient bundle are used in contraction and glueing operations used to construct vector bundles over quotient spaces.
A  -morphism of vector bundles
-morphism of vector bundles 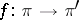 is said to be of constant rank (pure) if
is said to be of constant rank (pure) if  is locally constant on
is locally constant on  . Injective and surjective morphisms are exact and are said to be monomorphisms and epimorphisms of the vector bundle, respectively. The following vector bundles are uniquely defined for a morphism
. Injective and surjective morphisms are exact and are said to be monomorphisms and epimorphisms of the vector bundle, respectively. The following vector bundles are uniquely defined for a morphism 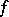 of locally constant rank:
of locally constant rank: 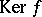 (the kernel of
(the kernel of 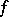 ), which is a subbundle of
), which is a subbundle of 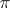 ;
; 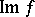 (the image of
(the image of 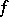 ), which is a subbundle of
), which is a subbundle of 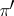 ;
; 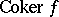 (the cokernel of
(the cokernel of 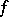 ), which is a quotient bundle of
), which is a quotient bundle of 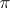 ; and
; and 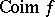 (the co-image of
(the co-image of 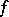 ), which is a quotient bundle of
), which is a quotient bundle of 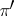 . Any subbundle
. Any subbundle 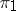 is the image of some monomorphism
is the image of some monomorphism  , while any quotient bundle
, while any quotient bundle 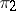 is the cokernel of some epimorphism
is the cokernel of some epimorphism 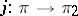 . A sequence of
. A sequence of  -morphisms of vector bundles
-morphisms of vector bundles
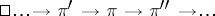 |
is said to be exact if the sequence
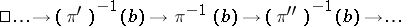 |
is exact for all 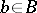 . In particular, the sequence
. In particular, the sequence
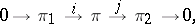 |
where  is the zero vector bundle, is exact if
is the zero vector bundle, is exact if 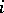 is a monomorphism,
is a monomorphism, 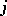 is an epimorphism and
is an epimorphism and 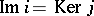 . The set of vector bundles over
. The set of vector bundles over  and
and 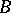 -morphisms of locally constant rank forms an exact subcategory
-morphisms of locally constant rank forms an exact subcategory 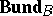 of the category
of the category  .
.
For any vector bundle 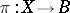 and mapping
and mapping 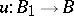 , the induced fibre bundle
, the induced fibre bundle 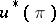 is endowed with a vector bundle structure such that the morphism
is endowed with a vector bundle structure such that the morphism 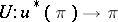 is a vector bundle morphism. This structure is unique and has the following property: Every fibre mapping
is a vector bundle morphism. This structure is unique and has the following property: Every fibre mapping 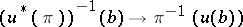 is an isomorphism of vector spaces. For instance, a vector bundle of dimension
is an isomorphism of vector spaces. For instance, a vector bundle of dimension 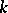 over a paracompact space
over a paracompact space 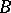 is isomorphic to one of the vector bundles
is isomorphic to one of the vector bundles 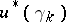 and
and 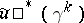 induced by certain mappings
induced by certain mappings 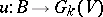 and
and 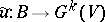 , respectively; moreover, homotopic mappings induce isomorphic vector bundles and, if
, respectively; moreover, homotopic mappings induce isomorphic vector bundles and, if 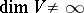 , the converse is true: To isomorphic vector bundles there correspond homotopic mappings
, the converse is true: To isomorphic vector bundles there correspond homotopic mappings  and
and 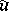 . This is one of the fundamental theorems in the homotopic classification of vector bundles, expressing the universal character of the vector bundles
. This is one of the fundamental theorems in the homotopic classification of vector bundles, expressing the universal character of the vector bundles 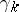 and
and 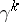 with respect to the classifying mappings
with respect to the classifying mappings  and
and 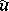 .
.
Any continuous operation (functor) 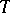 on the category of vector spaces uniquely determines a continuous functor on the category of vector bundles over
on the category of vector spaces uniquely determines a continuous functor on the category of vector bundles over 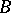 ; in this way it is possible to construct bundles associated with a given vector bundle: tensor bundles, vector bundles of morphisms
; in this way it is possible to construct bundles associated with a given vector bundle: tensor bundles, vector bundles of morphisms 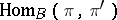 and, in particular, the dual vector bundle
and, in particular, the dual vector bundle 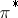 , exterior powers of vector bundles, etc., whose sections are vector bundles with supplementary structures. These are extensively employed in practical applications.
, exterior powers of vector bundles, etc., whose sections are vector bundles with supplementary structures. These are extensively employed in practical applications.
A direct sum (Whitney sum) 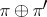 and tensor product
and tensor product 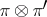 have been defined for two vector bundles
have been defined for two vector bundles 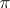 and
and 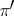 . With respect to these operations the set of classes
. With respect to these operations the set of classes 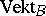 of isomorphic vector bundles over
of isomorphic vector bundles over 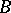 forms a semi-ring which plays an important part in the construction of a
forms a semi-ring which plays an important part in the construction of a 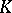 -functor; thus, if for vector bundles
-functor; thus, if for vector bundles 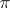 and
and 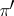 there exist trivial vector bundles
there exist trivial vector bundles 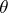 and
and 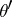 such that the vector bundles
such that the vector bundles 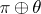 and
and 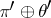 are isomorphic (i.e.
are isomorphic (i.e. 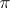 and
and 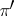 are stably equivalent), then their images in the "completion"
are stably equivalent), then their images in the "completion" 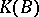 of the semi-ring
of the semi-ring 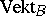 are identical; moreover, the fact that the ring
are identical; moreover, the fact that the ring 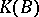 and the set of classes of stably-equivalent vector bundles coincide follows from the existence of an inverse vector bundle for any vector bundle over a paracompact space.
and the set of classes of stably-equivalent vector bundles coincide follows from the existence of an inverse vector bundle for any vector bundle over a paracompact space.
For any vector bundle 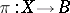 over a paracompact space
over a paracompact space 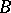 there exists a section
there exists a section 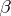 of the vector bundle
of the vector bundle
 |
where 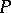 is a trivial one-dimensional vector bundle, which on each fibre
is a trivial one-dimensional vector bundle, which on each fibre 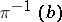 is a positive-definite form, i.e.
is a positive-definite form, i.e. 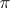 is metrizable; this makes it possible to establish, in particular, the splittability of an arbitrary exact sequence of vector bundles
is metrizable; this makes it possible to establish, in particular, the splittability of an arbitrary exact sequence of vector bundles
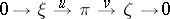 |
in which 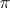 is metrizable, that is, the existence of a morphism
is metrizable, that is, the existence of a morphism 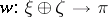 such that
such that  ,
, 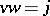 , where
, where 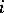 is the imbedding into the first term and
is the imbedding into the first term and  is the projection onto the second term.
is the projection onto the second term.
If, in each fibre 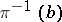 of the vector bundle
of the vector bundle 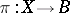 , one identifies the points lying on the same line passing through zero, one obtains a bundle
, one identifies the points lying on the same line passing through zero, one obtains a bundle 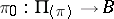 , which is associated with
, which is associated with 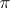 and is said to be its projectivization; a fibre of
and is said to be its projectivization; a fibre of 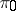 is the projective space
is the projective space  which is associated with
which is associated with 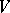 . This bundle is used to study Thom spaces
. This bundle is used to study Thom spaces 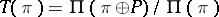 (cf. Thom space), used in the homotopic interpretation of classes of bordant manifolds, characteristic classes of vector bundles describing the homological properties of manifolds, etc.
(cf. Thom space), used in the homotopic interpretation of classes of bordant manifolds, characteristic classes of vector bundles describing the homological properties of manifolds, etc.
The concept of a vector bundle can be generalized to the case when the fibre is an infinite-dimensional vector space; in doing so, one must distinguish between the different topologies of the space of morphisms 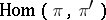 , suitably modify the definitions of a pure morphism and an exact sequence of morphisms, and also the construction of vector bundles associated with continuous functors on the category of infinite-dimensional vector spaces.
, suitably modify the definitions of a pure morphism and an exact sequence of morphisms, and also the construction of vector bundles associated with continuous functors on the category of infinite-dimensional vector spaces.
References
| [1] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) MR0242081 Zbl 0653.53001 Zbl 0284.53018 |
| [2] | M.F. Atiyah, "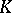 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [3] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III MR1931083 MR1532744 MR0155257 Zbl 1008.57001 Zbl 0103.15101 |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) MR0229247 Zbl 0144.44804 |
| [5] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) MR0533884 Zbl 0444.32004 |
| [6] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) MR1335917 MR0202713 Zbl 0376.14001 |
Comments
For more on the universality and classifying properties of the bundles 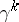 and
and 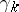 cf. Classifying space or [a1].
cf. Classifying space or [a1].
References
| [a1] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) MR0440554 Zbl 0298.57008 |
Multi-valued representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multi-valued_representation&oldid=12923