Difference between revisions of "Regular scheme"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.S. Abhyankar, "On the problem of resolution of singularities" I.G. Petrovskii (ed.) , ''Proc. Internat. Congress Mathematicians Moscow, 1966'' , Moscow (1968) pp. 469–481 {{MR|0232771}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) {{MR|0209285}} {{ZBL|0187.42701}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I, II" ''Ann. of Math.'' , '''79''' (1964) pp. 109–203; 205–326 {{MR|0199184}} {{ZBL|0122.38603}} </TD></TR></table> |
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 111–115; 126 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A scheme 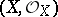 such that at every point the local ring
such that at every point the local ring  is regular (cf. Regular ring (in commutative algebra)). For schemes of finite type over an algebraically closed field
is regular (cf. Regular ring (in commutative algebra)). For schemes of finite type over an algebraically closed field 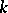 , regularity is equivalent to the sheaf of differentials
, regularity is equivalent to the sheaf of differentials 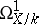 being locally free. Regular local rings are factorial (cf. Factorial ring), and so any closed reduced irreducible subscheme of codimension 1 in a regular scheme
being locally free. Regular local rings are factorial (cf. Factorial ring), and so any closed reduced irreducible subscheme of codimension 1 in a regular scheme 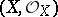 is given locally by one equation (see [2]). An important problem is the construction of a regular scheme
is given locally by one equation (see [2]). An important problem is the construction of a regular scheme 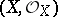 with a given field
with a given field 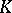 of rational functions and equipped with a proper morphism
of rational functions and equipped with a proper morphism 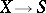 onto some base scheme
onto some base scheme 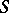 . The solution is known in the case when
. The solution is known in the case when 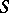 is the spectrum of a field of characteristic 0 (see [3]), and for schemes of low dimension in the case of a prime characteristic and also in the case when
is the spectrum of a field of characteristic 0 (see [3]), and for schemes of low dimension in the case of a prime characteristic and also in the case when 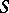 is the spectrum of a Dedekind domain with
is the spectrum of a Dedekind domain with 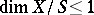 (see [1]).
(see [1]).
References
| [1] | S.S. Abhyankar, "On the problem of resolution of singularities" I.G. Petrovskii (ed.) , Proc. Internat. Congress Mathematicians Moscow, 1966 , Moscow (1968) pp. 469–481 MR0232771 |
| [2] | D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701 |
| [3] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. , 79 (1964) pp. 109–203; 205–326 MR0199184 Zbl 0122.38603 |
Comments
Sometimes a regular scheme is called a smooth scheme, in which case one means that the structure morphism 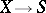 is a smooth morphism (where
is a smooth morphism (where 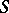 is the spectrum of a field, cf. Spectrum of a ring).
is the spectrum of a field, cf. Spectrum of a ring).
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 111–115; 126 MR0463157 Zbl 0367.14001 |
Regular scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_scheme&oldid=12959