Difference between revisions of "Markov chain, generalized"
From Encyclopedia of Mathematics
(MSC|60J10 Category:Markov chains) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.L. Doob, "Stochastic processes" , Wiley (1953) {{MR|1570654}} {{MR|0058896}} {{ZBL|0053.26802}} </TD></TR></table> |
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Freedman, "Markov chains" , Holden-Day (1975) {{MR|0686269}} {{MR|0681291}} {{MR|0556418}} {{MR|0428472}} {{MR|0292176}} {{MR|0237001}} {{MR|0211464}} {{MR|0164375}} {{MR|0158435}} {{MR|0152015}} {{ZBL|0501.60071}} {{ZBL|0501.60069}} {{ZBL|0426.60064}} {{ZBL|0325.60059}} {{ZBL|0322.60057}} {{ZBL|0212.49801}} {{ZBL|0129.30605}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) {{MR|1531032}} {{MR|0115196}} {{ZBL|0089.13704}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Revuz, "Markov chains" , North-Holland (1975) {{MR|0415773}} {{ZBL|0332.60045}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) {{MR|0266312}} {{ZBL|0201.20002}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) {{MR|2209438}} {{ZBL|0471.60001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> A. Blanc-Lapierre, R. Fortet, "Theory of random functions" , '''1–2''' , Gordon & Breach (1965–1968) (Translated from French) {{MR|}} {{ZBL|0185.44502}} {{ZBL|0159.45802}} </TD></TR></table> |
Revision as of 10:31, 27 March 2012
2020 Mathematics Subject Classification: Primary: 60J10 [MSN][ZBL]
A sequence of random variables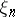 
with the properties:
1) the set of values of each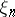 
is finite or countable;
2) for any 
and any 
,
 | (*) |
 |
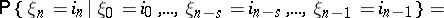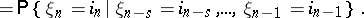A generalized Markov chain satisfying (*) is called 
-generalized. For 
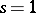, (*) is the usual Markov property. The study of 
-generalized Markov chains can be reduced to the study of ordinary Markov chains. Consider the sequence of random variables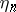 
whose values are in one-to-one correspondence with the values of the vector
 |
The sequence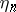 
forms an ordinary Markov chain.
References
| [1] | J.L. Doob, "Stochastic processes" , Wiley (1953) MR1570654 MR0058896 Zbl 0053.26802 |
Comments
References
| [a1] | D. Freedman, "Markov chains" , Holden-Day (1975) MR0686269 MR0681291 MR0556418 MR0428472 MR0292176 MR0237001 MR0211464 MR0164375 MR0158435 MR0152015 Zbl 0501.60071 Zbl 0501.60069 Zbl 0426.60064 Zbl 0325.60059 Zbl 0322.60057 Zbl 0212.49801 Zbl 0129.30605 |
| [a2] | J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) MR1531032 MR0115196 Zbl 0089.13704 |
| [a3] | D. Revuz, "Markov chains" , North-Holland (1975) MR0415773 Zbl 0332.60045 |
| [a4] | V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) MR0266312 Zbl 0201.20002 |
| [a5] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) MR2209438 Zbl 0471.60001 |
| [a6] | A. Blanc-Lapierre, R. Fortet, "Theory of random functions" , 1–2 , Gordon & Breach (1965–1968) (Translated from French) Zbl 0185.44502 Zbl 0159.45802 |
How to Cite This Entry:
Markov chain, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_generalized&oldid=21652
Markov chain, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_generalized&oldid=21652
This article was adapted from an original article by V.P. Chistyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article