Carathéodory-Toeplitz extension problem

Let 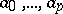be given complex numbers. The Carathéodory–Toeplitz extension problem is to find (if possible) a function 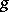, analytic on the open unit disc 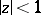(cf. also Analytic function), such that

a) , ;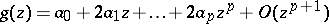

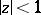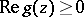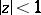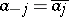b) for all . Put for 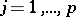. The problem is solvable if and only if the Toeplitz matrix

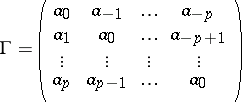(a1)

is positive semi-definite, and its solution is unique if and only if, in addition, is singular (cf. also Degenerate matrix). The Carathéodory–Toeplitz extension problem can be restated as a Carathéodory–Schur extension problem. The Levinson algorithm from filtering theory provides a recursive method to compute the solutions of the problem. For these and related results, see [a1], Chapt. 2.

Instead of functions 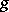satisfying a) and b), one may also seek functions , , 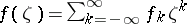in the Wiener algebra 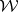with the property 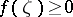for every 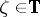. (The Wiener algebra is defined as the Banach algebra of complex-valued functions on the unit disc having a Fourier series

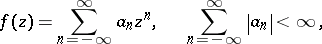using pointwise multiplication. The phrase "Wiener algebra" is also used for 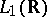with convolution as multiplication. There are also weighted versions; cf. [a2].)

In this case, 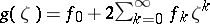satisfies conditions a) and b). The Wiener algebra version of the problem is of particular interest if the solution 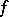is required to be strictly positive on the unit circle 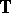. The latter version of the problem is solvable if and only if the Toeplitz matrix 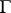in (a1) is positive definite, and in that case there are infinitely many solutions 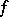, given by

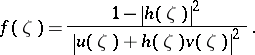(a2)

Here, 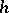is an arbitrary function in the Wiener algebra with 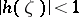for every 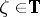, and the functions and are uniquely determined by the data in the following way:

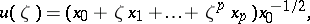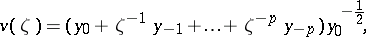where

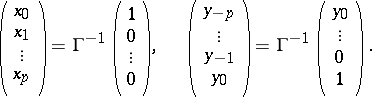The central solution 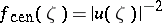, which appears when the free parameter 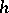in (a2) is set to zero, is the unique solution 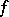with the additional property that the 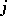th Fourier coefficient of 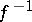is equal to zero for 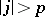, and for this reason the central solution is also referred to as the band extension. The central solution 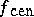is also the unique solution 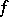that maximizes the entropy integral

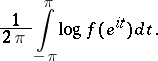Proofs of the above results may derived by applying the band method (see [a2], Sect. XXXV.3), which is a general scheme for dealing with a variety of positive and contractive (operator) extension problems from a unified point of view. (The word "band" refers to a decomposition of an algebra with involution, reminiscent of the use of bands as in the theory of decomposition or Riesz spaces (cf. Riesz space). It refers, in fact, to a "band pattern" , i.e. a band in a matrix 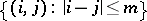, cf. also Partially specified matrices, completion of.)

The Carathéodory–Toeplitz extension problem has natural generalizations for matrix- and operator-valued functions. The problem also has a continuous analogue (with the role of the open unit disc being replaced by the upper half-plane) and non-stationary versions for finite or infinite operator matrices.

References

[a1]	C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990)
[a2]	I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators" , II , Birkhäuser (1993)