Difference between revisions of "Matsushima criterion"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> Y. Matsushima, "Espaces homogènes de Stein des groupes de Lie complexes" ''Nagoya Math. J.'' , '''16''' (1960) pp. 205–218 {{MR|0109854}} {{ZBL|0094.28201}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Białynicki-Birula, "On homogeneous affine spaces of linear algebraic groups" ''Amer. J. Math.'' , '''85''' (1963) pp. 577–582 {{MR|}} {{ZBL|0116.38202}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D. Luna, "Slices étales" ''Bull. Soc. Math. France'' , '''33''' (1973) pp. 81–105 {{MR|0342523}} {{ZBL|0286.14014}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A. Borel, Harish-Chandra, "Arithmetic subgroups of algebraic groups" ''Ann. of Math.'' , '''75''' (1962) pp. 485–535 {{MR|0147566}} {{ZBL|0107.14804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.A. Nisnevich, "Affine homogeneous spaces and finite subgroups of arithmetic groups over function fields" ''Funct. Anal. Appl.'' , '''11''' : 1 (1977) pp. 64–65 ''Funktsional. Anal. i Prilozhen.'' , '''11''' : 1 (1977) pp. 73–74 {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> R.W. Richardson, "Affine coset spaces of reductive algebraic groups" ''Bull. London Math. Soc.'' , '''9''' (1977) pp. 38–41 {{MR|0437549}} {{ZBL|0355.14020}} </TD></TR></table> |
Revision as of 14:50, 24 March 2012
The homogeneous space 
, where 
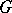is an affine reductive algebraic group (cf. also Affine group; Reductive group) defined over an algebraically closed field 
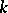and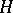 
is a closed subgroup of 
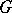, is an affine algebraic variety if and only if 
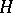is a reductive group. This criterion was first found by Y. Matsushima [1] in the case where 
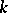is the complex field. Later, proofs were given that are valid for every algebraically closed field of characteristic zero (see [2], [3], [4]). In the case where the characteristic of 
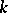is positive, the proof of the criterion was obtained only after the proof of the Mumford hypothesis (see [5], [6]).
References
| [1] | Y. Matsushima, "Espaces homogènes de Stein des groupes de Lie complexes" Nagoya Math. J. , 16 (1960) pp. 205–218 MR0109854 Zbl 0094.28201 |
| [2] | A. Białynicki-Birula, "On homogeneous affine spaces of linear algebraic groups" Amer. J. Math. , 85 (1963) pp. 577–582 Zbl 0116.38202 |
| [3] | D. Luna, "Slices étales" Bull. Soc. Math. France , 33 (1973) pp. 81–105 MR0342523 Zbl 0286.14014 |
| [4] | A. Borel, Harish-Chandra, "Arithmetic subgroups of algebraic groups" Ann. of Math. , 75 (1962) pp. 485–535 MR0147566 Zbl 0107.14804 |
| [5] | E.A. Nisnevich, "Affine homogeneous spaces and finite subgroups of arithmetic groups over function fields" Funct. Anal. Appl. , 11 : 1 (1977) pp. 64–65 Funktsional. Anal. i Prilozhen. , 11 : 1 (1977) pp. 73–74 |
| [6] | R.W. Richardson, "Affine coset spaces of reductive algebraic groups" Bull. London Math. Soc. , 9 (1977) pp. 38–41 MR0437549 Zbl 0355.14020 |
How to Cite This Entry:
Matsushima criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matsushima_criterion&oldid=19096
Matsushima criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matsushima_criterion&oldid=19096
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article