Difference between revisions of "Convergence in probability"
From Encyclopedia of Mathematics
(Importing text file) |
(MSC|60-01|28A20) |
||
| Line 1: | Line 1: | ||
| + | {{MSC|60-01|28A20}} | ||
| + | |||
Convergence of a sequence of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260801.png" /> defined on a probability space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260802.png" />, to a random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260803.png" />, defined in the following way: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260804.png" /> if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260805.png" />, | Convergence of a sequence of random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260801.png" /> defined on a probability space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260802.png" />, to a random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260803.png" />, defined in the following way: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260804.png" /> if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c026/c026080/c0260805.png" />, | ||
Revision as of 15:11, 7 February 2012
2020 Mathematics Subject Classification: Primary: 60-01 Secondary: 28A20 [MSN][ZBL]
Convergence of a sequence of random variables 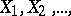 defined on a probability space
defined on a probability space 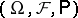 , to a random variable
, to a random variable 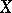 , defined in the following way:
, defined in the following way: 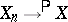 if for any
if for any 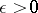 ,
,
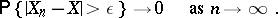 |
In mathematical analysis, this form of convergence is called convergence in measure. Convergence in distribution follows from convergence in probability.
Comments
See also Weak convergence of probability measures; Convergence, types of; Distributions, convergence of.
How to Cite This Entry:
Convergence in probability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_in_probability&oldid=15590
Convergence in probability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence_in_probability&oldid=15590
This article was adapted from an original article by V.I. Bityutskov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article