User:Rafael.greenblatt/sandbox

(starting to modify "Exterior algebra")

Grassmann algebra, of a vector space $V$ over a field $k$

An associative algebra over $k$, the operation in which is denoted by the symbol $\wedge$, with generating elements $1,e_1,\ldots,e_n$ where $e_1,\ldots,e_n$ is a basis of $V$, and with defining relations

$$ e_i \wedge e_j = - e_j \wedge e_i \qquad (i,j=1,\ldots,n), \qquad e_i \wedge e_i = 0, $$

$$ 1 \wedge e_i = e_i \wedge 1 = e_i \qquad (i=1,\ldots,n), \qquad \ \wedge 1 = 1. $$

The exterior algebra does not depend on the choice of the basis and is denoted by $\wedge V$. The subspace $\wedge^r V$ ($r=0,1,\ldots$) in $\wedge V$ generated by the elements of the form $e_{i_1} \wedge \ldots \wedge e_{i_r}$ is said to be the $r$-th exterior power of the space $V$. The following equalities are valid: $ \dim \wedge^r V = () = C_n^r$, $r=0,\ldots,n$, $\wedge^r V =0$, $r>n$. In addition, $v \wedge u = (-1)^{rs}u \wedge v$ if $u \in \wedge^r V$, $v \in \wedge^s V$. The elements of the space $\wedge^r V$ are said to be $r$-vectors; they may also be regarded as skew-symmetric $r$-times contravariant tensors in $V$ (cf. Exterior product).

$r$-vectors are closely connected with $r$-dimensional subspaces in $V$: Linearly independent systems of vectors $x_1,\ldots,x_r$ and $y_1,\ldots,y_r$ of $V$ generate the same subspace if and only if the $r$-vectors $x_1\wedge \ldots \wedge x_r$ and $y_1\wedge \ldots \wedge y_r$ are proportional. This fact served as one of the starting points in the studies of H. Grassmann [1], who introduced exterior algebras as the algebraic apparatus to describe the generation of multi-dimensional subspaces by one-dimensional subspaces. The theory of determinants is readily constructed with the aid of exterior algebras. An exterior algebra may also be defined for more general objects, viz. for unitary modules $M$ over a commutative ring $A$ with identity [4]. The $r$-th exterior power $\wedge^r M$, $r>0$, of a module $M$ is defined as the quotient module of the $r$-th tensor power of this module by the submodule generated by the elements of the form $x1 \otimes \ldots \otimes x_r$, where $x_i \in M$ and $x_j=x_k$ for certain $j \ne k$. The exterior algebra for $M$ is defined as the direct sum $\wedge M = \bigoplus_{r \ge 0}\wedge^r M$, where $\wedge^0 M = A$, with the naturally introduced multiplication. In the case of a finite-dimensional vector space this definition and the original definition are identical. The exterior algebra of a module is employed in the theory of modules over a principal ideal ring [5].

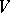The Grassmann (or Plücker) coordinates of an $r$-dimensional subspace $L$ in an $n$-dimensional space $V$ over $k$ are defined as the coordinates of the $r$-vector in $V$ corresponding to $L$, which is defined up to proportionality. Grassmann coordinates may be used to naturally imbed the set of all -dimensional subspaces in into the projective space of dimension 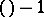, where it forms an algebraic variety (called the Grassmann manifold). Thus one gets several important examples of projective algebraic varieties [6].

Exterior algebras are employed in the calculus of exterior differential forms (cf. Differential form) as one of the basic formalisms in differential geometry [7], [8]. Many important results in algebraic topology are formulated in terms of exterior algebras.

E.g., if 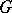is a finite-dimensional 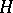-space (e.g. a Lie group), the cohomology algebra 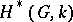of 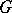with coefficients in a field 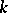of characteristic zero is an exterior algebra with odd-degree generators. If 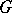is a simply-connected compact Lie group, then the ring 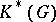, studied in 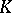-theory, is also an exterior algebra (over the ring of integers).

References

[1]	H. Grassmann, "Gesammelte mathematische und physikalische Werke" , 1 , Teubner (1894–1896) pp. Chapt. 1; 2
[2]	A.I. Mal'tsev, "Foundations of linear algebra" , Freeman (1963) (Translated from Russian)
[3]	L.A. Kaluzhnin, "Introduction to general algebra" , Moscow (1973) (In Russian)
[4]	N. Bourbaki, "Elements of mathematics. Algebra: Multilinear algebra" , Addison-Wesley (1966) pp. Chapt. 2 (Translated from French)
[5]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French)
[6]	W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1–3 , Cambridge Univ. Press (1947–1954)
[7]	S.P. Finikov, "Cartan's method of exterior forms in differential geometry" , 1–3 , Moscow-Leningrad (1948) (In Russian)
[8]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964)

Comments

Anticommuting variables (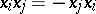, 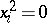) are sometimes called Grassmann variables; especially in the context of superalgebras, super-manifolds, etc. (cf. Super-manifold; Superalgebra). In addition the phrase fermionic variables occurs; especially in theoretical physics.

References

[a1]	C. Chevalley, "The construction and study of certain important algebras" , Math. Soc. Japan (1955)