User:Maximilian Janisch/latexlist/Algebraic Groups/Unipotent element
An element  of a linear algebraic group $k$ which coincides with the unipotent part $\sigma _ { n }$ of its Jordan decomposition in $k$. If $k$ is realized as a closed subgroup of the group $GL ( V )$ of automorphisms of a finite-dimensional vector space $V$ over an algebraically closed ground field $K$, then a unipotent element
of a linear algebraic group $k$ which coincides with the unipotent part $\sigma _ { n }$ of its Jordan decomposition in $k$. If $k$ is realized as a closed subgroup of the group $GL ( V )$ of automorphisms of a finite-dimensional vector space $V$ over an algebraically closed ground field $K$, then a unipotent element  is precisely an element
is precisely an element 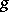 satisfying $( g - 1 ) ^ { n } = 0$, $n = \operatorname { dim } V$, or, equivalently, is such that its matrix relative to a certain basis of $V$ is upper triangular, with 1's on the main diagonal. The set $U ( G )$ of all unipotent elements in $k$ is closed in the Zariski topology. If $K = 0$, then every unipotent element
satisfying $( g - 1 ) ^ { n } = 0$, $n = \operatorname { dim } V$, or, equivalently, is such that its matrix relative to a certain basis of $V$ is upper triangular, with 1's on the main diagonal. The set $U ( G )$ of all unipotent elements in $k$ is closed in the Zariski topology. If $K = 0$, then every unipotent element 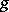 has infinite order. In that case the smallest algebraic subgroup of $k$ containing
has infinite order. In that case the smallest algebraic subgroup of $k$ containing 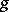 is a one-dimensional unipotent group. If, however, $K = p > 0$, then
is a one-dimensional unipotent group. If, however, $K = p > 0$, then 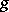 will be unipotent precisely when it has finite order $p ^ { t }$ for some $t \geq 0$. A connected group contains no unipotent element $g \neq \theta$ if and only if it is an algebraic torus.
will be unipotent precisely when it has finite order $p ^ { t }$ for some $t \geq 0$. A connected group contains no unipotent element $g \neq \theta$ if and only if it is an algebraic torus.
A criterion for anisotropy may be given in terms of unipotent elements (cf. Anisotropic group).
Unipotent elements play an important role in the theory of discrete subgroups (cf. Discrete subgroup) of algebraic groups and Lie groups. The presence of unipotent elements in a discrete group $I$ of motions of a symmetric space, having a non-compact fundamental domain of finite volume, is an important tool for studying the structure of such groups and their fundamental domains, cf. [5]; the existence of unipotent elements in such $I$ was proved in [4].
The variety $U ( G )$ is invariant under inner automorphisms of the group $k$. Let $k$ be connected and semi-simple. Then the number of conjugacy classes of unipotent elements is finite and for every simple $k$ there is a complete description of them (as well as a description of the centralizer of a unipotent element), cf. [7]. In the classical groups such a description is obtained by means of the Jordan form of matrices, [2]. E.g. for the group $G = SL _ { n } ( K )$ there exists a bijection between the conjugacy classes of unipotent elements and the partitions $( m _ { 1 } , \dots , m _ { s } )$ of $12$ into positive integers $m$, $m _ { 1 } \geq \ldots \geq m _ { s }$. If $\lambda = ( m _ { 1 } , \dots , m _ { s } )$ and $\mu = ( l _ { 1 } , \dots , l _ { t } )$ are two partitions of $12$, then the class corresponding to $2$ contains in its closure the class corresponding to $\mu$ precisely if $\sum _ { i = 1 } ^ { j } m _ { i } \geq \sum _ { i = 1 } ^ { j } l _ { i }$ for all $i$. The dimension of the class corresponding to the partition $( m _ { 1 } , \dots , m _ { s } )$ (as an algebraic variety) is equal to $n ^ { 2 } - \sum _ { i j } \operatorname { min } ( m _ { i } , m _ { j } )$.
The set of all simple points of the algebraic variety $U ( G )$ forms one conjugacy class of unipotent elements, the regular unipotent elements. If $k$ is simple, then the variety of singular points in the variety $U ( G )$ also contains a Zariski-open conjugacy class of unipotent elements — the subregular unipotent elements. For a study of the singular points of the variety $U ( G )$ see also [6].
References
| [1] | A. Borel, "Linear algebraic groups" , Springer (1991) MR1102012 Zbl 0726.20030 |
| [2] | A. Borel (ed.) R. Carter (ed.) C.W. Curtis (ed.) N. Iwahori (ed.) T.A. Springer (ed.) R. Steinberg (ed.) , Seminar on algebraic groups and related finite groups , Lect. notes in math. , 131 , Springer (1970) Zbl 0192.36201 |
| [3] | J.E. Humphreys, "Linear algebraic groups" , Springer (1981) MR0610979 MR0396773 Zbl 0471.20029 |
| [4] | D.A. Kazhdan, G.A. Margulis, "A proof of Selberg's hypothesis" Math. USSR Sb. , 4 : 1 (1969) pp. 147–152 Mat. Sb. , 75 : 1 (1968) pp. 163–168 |
| [5] | A. Selberg, "Recent developments in the theory of discontinuous groups of motions of symmetric spaces" , Proc. 15 Scand. Congress (Oslo, 1968) , Lect. notes in math. , 118 , Springer (1970) pp. 99–120 MR0263996 Zbl 0197.18002 |
| [6] | P.J. Slodowy, "Simple singularities and simple algebraic groups" , Lect. notes in math. , 815 , Springer (1980) MR0584445 Zbl 0441.14002 |
| [7] | N. Spaltenstein, "Classes unipotentes et sousgroupes de Borel" , Lect. notes in math. , 946 , Springer (1982) MR672610 |
Comments
References
| [a1] | T.A. Springer, "Linear algebraic groups" W. Jäger (ed.) J. Moser (ed.) R. Remmert (ed.) , Perspectives in Mathematics , Birkhäuser (1984) pp. 455–496 MR0779686 Zbl 0564.20024 |
Maximilian Janisch/latexlist/Algebraic Groups/Unipotent element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Unipotent_element&oldid=44069