User:Maximilian Janisch/latexlist/Algebraic Groups/Relative root system

This page is a copy of the article Relative root system in order to test automatic LaTeXification. This article is not my work.

of a connected reductive algebraic group $k$ defined over a field $k$

A system $\Phi _ { k } ( S , G )$ of non-zero weights of the adjoint representation of a maximal $k$-split torus $5$ of the group $k$ in the Lie algebra $8$ of this group (cf. Weight of a representation of a Lie algebra). The weights themselves are called the roots of $k$ relative to $5$. The relative root system $\Phi _ { k } ( S , G )$, which can be seen as a subset of its linear envelope $L$ in the space $X ( S ) \otimes _ { Z } R$, where $X ( S )$ is the group of rational characters of the torus $5$, is a root system. Let $N ( S )$ be the normalizer and $Z ( S )$ the centralizer of $5$ in $k$. Then $Z ( S )$ is the connected component of the unit of the group $N ( S )$; the finite group $W _ { k } ( S , G ) = N ( S ) / Z ( S )$ is called the Weyl group of $k$ over $k$, or the relative Weyl group. The adjoint representation of $N ( S )$ in $8$ defines a linear representation of $W _ { k } ( S , G )$ in $L$. This representation is faithful and its image is the Weyl group of the root system $\Phi _ { k } ( S , G )$, which enables one to identify these two groups. Since two maximal $k$-split tori $S _ { 1 }$ and $S _ { 2 }$ in $k$ are conjugate over $k$, the relative root systems $\Phi _ { k } ( S _ { l } , G )$ and the relative Weyl groups $W _ { k } ( S _ { i } , G )$, $i = 1,2$, are isomorphic, respectively. Hence they are often denoted simply by $\Phi _ { k } ( G )$ and $W _ { k } ( G )$. When $k$ is split over $k$, the relative root system and the relative Weyl group coincide, respectively, with the usual (absolute) root system and Weyl group of $k$. Let $g _ { a }$ be the weight subspace in $8$ relative to $5$, corresponding to the root $\alpha \in \Phi _ { k } ( S , G )$. If $k$ is split over $k$, then $g _ { \alpha } = 1$ for any $6$, and $\Phi _ { k } ( G )$ is a reduced root system; this is not so in general: $\Phi _ { k } ( G )$ does not have to be reduced and 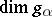can be greater than 1. The relative root system $\Phi _ { k } ( G )$ is irreducible if $k$ is simple over $k$.

The relative root system plays an important role in the description of the structure and in the classification of semi-simple algebraic groups over $k$. Let $k$ be semi-simple, and let $T$ be a maximal torus defined over $k$ and containing $5$. Let $X ( S )$ and $X ( T )$ be the groups of rational characters of the tori $5$ and $T$ with fixed compatible order relations, let $\Delta$ be a corresponding system of simple roots of $k$ relative to $T$, and let $\Delta _ { 0 }$ be the subsystem in $\Delta$ consisting of the characters which are trivial on $5$. Moreover, let $\Delta _ { k }$ be the system of simple roots in the relative root system $\Phi _ { k } ( S , G )$ defined by the order relation chosen on $X ( S )$; it consists of the restrictions to $5$ of the characters of the system $\Delta$. The Galois group $\Gamma = \operatorname { Gal } ( k _ { s } / k )$ acts naturally on $\Delta$, and the set $[ - \infty , - 1 ]$ is called the $k$-index of the semi-simple group $k$. The role of the $k$-index is explained by the following theorem: Every semi-simple group over $k$ is uniquely defined, up to a $k$-isomorphism, by its class relative to an isomorphism over $k _ { S }$, its $k$-index and its anisotropic kernel. The relative root system $\Phi _ { k } ( G )$ is completely defined by the system $\Delta _ { k }$ and by the set of natural numbers $n _ { Q }$, $\alpha \in \Delta k$ (equal to 1 or 2), such that $n _ { \alpha } \alpha \in \Phi _ { k } ( G )$ but $( n _ { \alpha } + 1 ) \alpha \notin \Phi _ { k } ( G )$. Conversely, $\Delta _ { k }$ and $n _ { Q }$, $\alpha \in \Delta k$, can be determined from the $k$-index. In particular, two elements from $\Delta \backslash \Delta _ { 0 }$ have one and the same restriction to $5$ if and only if they are located in the same orbit of $I$; this defines a bijection between $\Delta _ { k }$ and the set of orbits of $I$ into $\Delta \backslash \Delta _ { 0 }$.

If $\gamma \in \Delta _ { k }$, if $O _ { \gamma } \subset \Delta \backslash \Delta _ { 0 }$ is the corresponding orbit, if $\Delta ( \gamma )$ is any connected component in $\Delta _ { 0 } \cup O _ { \gamma }$ not all vertices of which lie in $\Delta _ { 0 }$, then $n$ is the sum of the coefficients of the roots $\alpha \in \Delta ( \gamma ) \cap O _ { \gamma }$ in the decomposition of the highest root of the system $\Delta ( \gamma )$ in simple roots.

If $k = R$, $\overline { k } = C$, then the above relative root system and relative Weyl group are naturally identified with the root system and Weyl group, respectively, of the corresponding symmetric space.

References

[1]	J. Tits, "Sur la classification des groupes algébriques semi-simples" C.R. Acad. Sci. Paris , 249 (1959) pp. 1438–1440 MR0106967
[2]	A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150 MR0207712 Zbl 0145.17402
[3]	J. Tits, "Classification of algebraic simple groups" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 33–62