User:Maximilian Janisch/latexlist/Algebraic Groups/Principal analytic fibration

This page is a copy of the article Principal analytic fibration in order to test automatic LaTeXification. This article is not my work.

A locally trivial analytic fibration on the fibres of which the structure Lie group acts simply transitively and analytically. In other words, a principal analytic fibration is a quadruple $( P , B , G , \pi )$ where $P$ and $B$ are analytic spaces (cf. Analytic space) over a field $k$; $\pi : P \rightarrow B$ is an analytic mapping; $k$ is a Lie group over $k$ analytically acting on $P$ from the right; and for each element of the base $B$ there exist a neighbourhood $r$ and an analytic isomorphism

\begin{equation} \phi : U \times G \rightarrow \pi ^ { - 1 } ( U ) \end{equation}

such that

\begin{equation} \phi ( x , g h ) = \phi ( x , g ) h , \quad x \in U , \quad g , h \in G \end{equation}

Each analytic vector bundle (cf. Vector bundle, analytic) $p : V \rightarrow B$ with $12$-dimensional fibre determines a principal analytic fibration with base $B$ and group $GL ( n , k )$, whose fibre over a point $b \in B$ is the variety of all bases of the fibre $p ^ { - 1 } ( b )$. This is a special case of a one-to-one correspondence between analytic fibrations with given fibre and structure group $k$ and the principal analytic fibrations associated with them. Other examples of principal analytic fibrations include the fibration $H \rightarrow H / G$ whose fibres are the left cosets of the Lie group $H$ by a Lie subgroup $k$ of it, and an analytic covering (here, the group of the covering is the structure group).

A principal analytic fibration can be defined by an open covering $\{ U _ { i } \} _ { i \in I }$ of its base $B$ and transition functions, i.e. analytic mappings

\begin{equation} g j : U _ { i } \cap U _ { j } \rightarrow G , \quad i , j \in I , \quad U _ { i } \cap U _ { j } \neq \emptyset \end{equation}

which satisfy the conditions

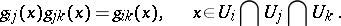The transition functions form a one-dimensional cocycle with values in the sheaf $o ^ { G }$ of germs of analytic mappings $B \rightarrow G$. This yields a one-to-one correspondence between the set of principal analytic fibrations with base $B$ and group $k$ and the set of cohomology spaces $H ^ { 1 } ( B , O ^ { G } )$. The classification of the principal analytic fibrations with base $B$ and structure group $k$ (in the case of a non-Abelian group $k$) is a problem which has so far been solved in a number of cases only (cf. Deformation of an analytic structure, for the corresponding local moduli problem). The connection between this classification and the classification of principal topological fibrations is expressed by the natural mapping

\begin{equation} \alpha : H ^ { 1 } ( B , O ^ { G } ) \rightarrow H ^ { 1 } ( B , C ^ { G } ) \end{equation}

where $C ^ { G }$ is the sheaf of germs of continuous mappings $B \rightarrow G$.

Let $k = C$, and let $B$ be a reduced Stein space; the mapping $6$ is then bijective, and the classification problem is reduced to a problem in homotopy theory [4]. In particular, any principal analytic fibration with a non-compact Riemann surface as base and with a connected structure group is trivial. The result of [4] was in fact obtained for the broader class of $k$-principal fibrations, in the definition of which the group $k$ is replaced by some locally trivial analytic fibration $E \rightarrow B$ on complex Lie groups, acting fibre-wise on $P$. This result has been generalized to the case when the structure group is a complex Banach Lie group [2]. If, on the other hand, $B$ is a compact Riemann surface, then $6$ is surjective and not injective. In the general case $6$ need not be either surjective nor injective. Sufficient cohomological conditions for $6$ to be injective or surjective are known [3] for a connected solvable group $k$.

The case when $B$ is a compact Riemann surface of genus $D$ and $k$ is a connected reductive algebraic group has been also studied. See [5] for the corresponding classification for $p = 0$; see [1] for the corresponding classification for $p = 1$ when $G = GL ( n , C )$. In the case $p \geq 2$, $G = GL ( n , C )$ (cf. Vector bundle, algebraic) an important role is played by the concept of a stable vector bundle. This concept has been generalized [6] to the case of an arbitrary connected reductive group $k$. The set of all stable principal fibrations of a given topological type on a compact Riemann surface has the natural structure of a connected normal analytic space. A partial classification of vector bundles over the complex projective space $B = P ^ { m } ( C )$ and over algebraic surfaces has also been obtained.

See Real-analytic space for real principal analytic fibrations (the case $k = R$).

References

[1]	M.F. Atiyah, "Vector bundles over an elliptic curve" Proc. London Math. Soc. (3) , 7 (1957) pp. 414–452 MR0131423 Zbl 0084.17305
[2]	L. Bungart, "On analytic fibre bundles - I. Holomorphic fibre bundles with infinite dimensional fibres" Topology , 7 (1968) pp. 55–68 MR0222338 MR0201673
[3]	J. Frenkel, "Cohomologie non Abélienne et espaces fibrés" Bull. Soc. Math. France , 85 (1957) pp. 135–220 MR0098200 Zbl 0082.37702
[4]	H. Grauert, "Analytische Faserungen über holomorph-vollständigen Räumen" Math. Ann. , 135 (1958) pp. 263–273 MR0098199 Zbl 0081.07401
[5]	A. Grothendieck, "Sur la classification des fibres holomorphes sur la sphere de Riemann" Amer. J. Math. , 79 (1957) pp. 121–138 MR0087176 Zbl 0079.17001
[6]	A. Ramanathan, "Stable principal bundles on a compact Riemann surface" Math. Ann. , 213 (1975) pp. 129–152 MR0369747 Zbl 0284.32019

Comments

For the partial classification of bundles over a complex projective space or an algebraic surface see [a1]–[a3].

References

[a1]	A. van de Ven, "Twenty years of classifying algebraic vectorbundles" A. Beauville (ed.) , Journées de géometrie algébrique d'Angers , Sijthoff & Noordhoff (1980) pp. 3–20
[a2]	R. Harshorne, "Four years of algebraic vectorbundles" A. Beauville (ed.) , Journées de géometrie algébrique d'Angers (1979) , Sijthoff & Noordhoff (1980) pp. 21–29
[a3]	C. Okonek, M. Schneider, H. Spindler, "Vector bundles on complex projective spaces" , Birkhäuser (1980) MR0561910 Zbl 0438.32016