User:Maximilian Janisch/latexlist/Algebraic Groups/Picard scheme

This page is a copy of the article Picard scheme in order to test automatic LaTeXification. This article is not my work.

A natural generalization of the concept of the Picard variety $F ( X )$ for a smooth algebraic variety $x$ within the framework of the theory of schemes. To define the Picard scheme for an arbitrary $5$-scheme $x$ one considers the relative Picard functor $PICX / S$ in the category $\operatorname { sch } / S$ of schemes over the scheme $5$. The value of this functor on an $5$-scheme $S ^ { \prime }$ is the group

where $f ^ { \prime } : X \times s S ^ { \prime } \rightarrow S ^ { \prime }$ is the base-change morphism and 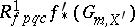is the sheaf in the Grothendieck topology $S _ { f } ^ { \prime } p q c$ of strictly-flat quasi-compact morphisms associated with the pre-sheaf

\begin{equation} T \rightarrow H ^ { 1 } ( T _ { f } p q c , G _ { m } ) = H ^ { 1 } ( T _ { et } , G _ { m } ) \end{equation}

and $G _ { m }$ denotes the standard multiplicative group sheaf. If the Picard functor $PICX / S$ is representable on $\operatorname { sch } / S$, then the $5$-scheme representing it is called the relative Picard scheme for the $5$-scheme $x$ and is denoted by $x / S$. If $x$ is an algebraic scheme over a certain field $k$ having a rational $k$-point, then

\begin{equation} \operatorname { Pic } _ { X / k } ( S ^ { \prime } ) = \operatorname { Fic } ( X \times k S ^ { \prime } ) / \operatorname { Fic } ( S ^ { \prime } ) \end{equation}

for any $k$-scheme $S ^ { \prime }$ [3]. In particular, $k ( k ) = \operatorname { Pic } ( X )$ can be identified with the group of $k$-rational points $\operatorname { Pic } _ { X / k } ( k )$ of $PICX / K$ if such exists.

If $f : X \rightarrow S$ is a projective morphism with geometrically-integral fibres, then the scheme $x / S$ exists and is a locally finitely representable separable group $5$-scheme. If $S = \operatorname { Spec } ( k )$, then the connected component of the unit, $\operatorname { Pic } _ { X / k } ^ { 0 }$, of $x / k$ is an algebraic $k$-scheme, and the corresponding reduced $k$-scheme is precisely the Picard variety $P _ { c } ( X )$ [4]. The nilpotent elements in the local rings of the scheme $\operatorname { Pic } _ { X / k } ^ { 0 }$ give much additional information on the Picard scheme and enable one to explain various "pathologies" in algebraic geometry over a field of characteristic $p > 0$. On the other hand, over a field of characteristic 0 the scheme $\operatorname { Pic } _ { K / k } ^ { Q }$ is always reduced [6]. It is also known that $PICF / k$ is a reduced scheme if $H ^ { \prime }$ is a smooth algebraic surface and $H ^ { 2 } ( F , O _ { F } ) = 0$ [5].

For any proper flat morphism $f : X \rightarrow S$ (finitely representable if the base $5$ is Noetherian) for which $f ^ { \prime } ( O _ { X ^ { \prime } } ) = O _ { S ^ { \prime } }$, the functor $PICX / S$ is an algebraic space over $5$ for any base-change morphism $f ^ { \prime } : X ^ { \prime } = X \times S S ^ { \prime } \rightarrow S$ [1]. In particular, the functor $PICX / S$ is representable if the ground scheme $5$ is the spectrum of a local Artinian ring.

References

[1]	M. Artin, "Algebraization of formal moduli I" D.C. Spencer (ed.) S. Iyanaga (ed.) , Global analysis (papers in honor of K. Kodaira) , Univ. Tokyo Press (1969) pp. 21–72 MR0260746 Zbl 0205.50402
[2]	C. Chevalley, "Sur la théorie de la variété de Picard" Amer. J. Math. , 82 (1960) pp. 435–490 MR0118723 Zbl 0127.37701
[3]	A. Grothendieck, "Technique de déscente et théorèmes d'existence en géometrie algébrique. V. Les schémas de Picard. Théorèmes d'existence" Sém. Bourbaki , 14 (1962) pp. 232/01–232/19 MR1611170
[4]	A. Grothendieck, "Eléments de géomètrie algébrique. I Le langage des schémas" Publ. Math. IHES : 4 (1960) pp. 1–228 MR0217083 MR0163908 Zbl 0118.36206
[5]	D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966) MR0209285 Zbl 0187.42701
[6]	F. Oort, "Algebraic group schemes in character zero are reduced" Invent. Math. , 2 : 1 (1966) pp. 79–80 MR206005
[7]	I.V Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 : 3 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 10 (1972) pp. 47–112 Zbl 1068.14059

Comments

The standard multiplicative sheaf over a scheme $x$ assigns to an affine open set $r$ in $x$ the group $\Gamma ( U , O _ { X } ) ^ { * }$ of units of $\Gamma ( U , O _ { X } )$.

References

[a1]	A. Grothendieck, "Fondements de la géométrie algébrique" , Secr. Math. Univ. Paris (1961/62) (Extracts Sem. Bourbaki 1957–1962) MR1611235 MR1086880 MR0146040 Zbl 0239.14002 Zbl 0239.14001
[a2]	A. Altman, S. Kleiman, "Compactification of the Picard scheme I" Adv. in Math. , 35 (1980) pp. 50–112
[a3]	A. Altman, S. Kleiman, "Compactification of the Picard scheme II" Amer. J. Math. , 101 (1979) pp. 10–41
[a4]	J.P. Murre, "On contravariant functors from the category of preschemes over a field into the category of abelian groups (with an application to the Picard functor)" Publ. Math. IHES , 23 (1964) pp. 581–619 MR206011 Zbl 0142.18402
[a5]	F. Oort, "Sur le schéma de Picard" Bull. Soc. Math. France , 90 (1962) pp. 1–14 MR0138627 Zbl 0123.13901