User:Maximilian Janisch/latexlist/Algebraic Groups/Invariants, theory of
(in the classical sense), invariant theory
The algebraic theory (sometimes called the algebraic theory of invariants) that studies algebraic expressions (polynomials, rational functions or families of them) that change in a specified way under non-degenerate linear changes of variables. Here, in general one does not consider the general linear group (that is, the entire set of non-degenerate linear changes of variables), but only a certain subgroup of it (for example, the orthogonal, the symplectic, etc., subgroup). The theory of invariants arose from a number of problems in number theory, algebra and geometry. C.F. Gauss in his studies on the theory of binary quadratic forms posed the problem of studying polynomials in the coefficients of the form $a x ^ { 2 } + 2 b x y + c y ^ { 2 }$ that do not change under transformations of these coefficients induced by substitutions of the form $X \rightarrow \alpha X + \beta y$, $y \rightarrow \gamma x + \delta y$, where $\alpha \delta - \beta \gamma = 1$ and $6$, $3$, $m$, $0$ are integers. On the other hand, in the intrinsic characterization of configurations and relations in projective geometry there occur algebraic expressions of projective coordinates that do not change under projective collineations. The study of determinants also preceded the theory of invariants. Arithmetic and algebraic questions, connected in one way or another with the theory of invariants, drew the attention of C.G.J. Jacobi, F. Eisenstein and Ch. Hermite. The theory of invariants was formed as a mathematical discipline in the mid-19th century. This period is characterized by an interest in formal algebraic problems and their applications to geometry. The notions of a group, an invariant and the fundamental problems of the theory were formulated at that time in a precise manner and gradually it became clear that various facts of classical and projective geometry are merely expressions of identities (syzygies) between invariants or covariants of the corresponding transformation groups. The Memoir on hyperdeterminants by A. Cayley (1846) must apparently be regarded as the first work on the theory of invariants. All the regular terms in the theory of invariants such as invariant; covariant; comitant; discriminant, etc., were introduced by J. Sylvester.
One of the first objects of study in invariant theory were the so-called invariants of forms. One considers a form of degree $N$ in $12$ variables with undetermined coefficients:
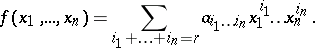 |
After the linear change of variables
\begin{equation} x _ { i } \rightarrow \sum _ { j = 1 } ^ { n } \alpha _ { i j } x _ { j } , \quad 1 \leq i \leq n \end{equation}
where $\alpha _ { i j }$ are real or complex numbers, it is converted to the form
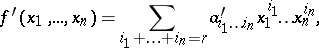 |
so that the above linear transformation of variables determines a transformation of the coefficients of the form:
\begin{equation} \alpha _ { 1 } , \ldots , i _ { R } \rightarrow \alpha _ { 2 } ^ { \prime } , \ldots , i _ { R } \end{equation}
A polynomial 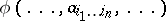 in the coefficients of the form $f ( x _ { 1 } , \ldots , x _ { x } )$ is called a (relative) invariant of the form if the following relation holds under any non-degenerate linear change of variables:
in the coefficients of the form $f ( x _ { 1 } , \ldots , x _ { x } )$ is called a (relative) invariant of the form if the following relation holds under any non-degenerate linear change of variables:
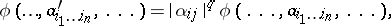 |
where $| \alpha _ { i j } |$ is the determinant of the linear transformation and $h$ is a constant (the weight). If $q = 0$, the invariant is called absolute. E.g., the simplest example of an invariant is the discriminant $D = b ^ { 2 } - a c$ of the binary quadratic ($n = r = 2$) form $f ( x , y ) = a x ^ { 2 } + 2 b x y + c y ^ { 2 }$, or the discriminant $\Delta = 3 b ^ { 2 } c ^ { 2 } + 6 a b c d - 4 b ^ { 3 } d - 4 a c ^ { 3 } - a ^ { 2 } d ^ { 2 }$ of the ternary ($n = 2$, $r = 3$) form $f ( x , y ) = a x ^ { 3 } + 3 b x ^ { 2 } y + 3 c x y ^ { 2 } + d y ^ { 3 }$. If one is given not one but several forms in the same set of variables, then it is possible to consider polynomials $( 1 )$ in the coefficients of all these forms transforming in the above manner under a linear change of variables; in this way one obtains the notion of a joint invariant of a system of forms. For example, the determinant $| \alpha _ { i j } |$ is a joint invariant of the system of $12$ linear forms $f _ { i } ( x _ { 1 } , \ldots , x _ { n } ) = \sum _ { j = 1 } ^ { n } a _ { j } x _ { j }$, $1 \leq i \leq n$. Similarly one can define a covariant and, more generally, a comitant.
The classical statement of the fundamental problem in the theory of invariants is to calculate the invariants, and also to give a complete description of them (and the same for covariants). To this end, various formal processes were developed enabling one to construct invariants (polarization, restitution, the Capelli identity, the Cayley $S$-process, etc.). The culmination of this activity was the creation of the so-called symbolic method in the theory of invariants, which is a formal method for calculating all the invariants of degree not exceeding a given number (see [3], [6], [11]).
The global theory of semi-simple groups and their representations, developed in the 1930's, has enabled one to give the following more general statement of the fundamental problem in the classical theory of invariants [6]. One is given an arbitrary group $k$ and a finite-dimensional linear representation $0$ of it in a linear space $V$ over a field $k$. If $x _ { 1 } , \ldots , x _ { x }$ are coordinates in $V$ (in some basis), then each element $g \in G$ determines a linear change of the variables $x _ { 1 } , \ldots , x _ { x }$; by carrying out this change of variables in an arbitrary polynomial $\phi ( x _ { 1 } , \ldots , x _ { x } )$ one obtains a new polynomial, hence 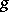 induces a transformation (automorphism) of the ring of all polynomials $k [ x _ { 1 } , \ldots , x _ { y } ]$ in the variables $x _ { 1 } , \ldots , x _ { x }$ over the field $k$. A polynomial $\phi ( x _ { 1 } , \ldots , x _ { x } )$ that does not change under all such transformations (that is, when
induces a transformation (automorphism) of the ring of all polynomials $k [ x _ { 1 } , \ldots , x _ { y } ]$ in the variables $x _ { 1 } , \ldots , x _ { x }$ over the field $k$. A polynomial $\phi ( x _ { 1 } , \ldots , x _ { x } )$ that does not change under all such transformations (that is, when 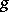 runs through the whole of $k$) is called an invariant of the representation $0$ of the group $k$ (cf. also Linear representation, invariant of a). All the invariants form a $k$-algebra and the aim of the theory of invariants is to describe this algebra. Thus, the invariants of forms are the invariants of the general linear group with respect to its representation in the space of symmetric tensors of fixed rank of the underlying (or dual) space (the coefficients of the original form $f$ are the components of this tensor); the consideration of covariants reduces to the study of the algebra of invariants for a representation in the space of tensors of mixed valency. In this form the problem of the description of invariants is a special case of the following general problem of the theory of linear representations: To decompose a space of tensors of given valency into irreducible invariant subspaces with respect to a given group of linear transformations of the underlying linear space (the search for invariants can be reduced to singling out the one-dimensional invariant subspaces).
runs through the whole of $k$) is called an invariant of the representation $0$ of the group $k$ (cf. also Linear representation, invariant of a). All the invariants form a $k$-algebra and the aim of the theory of invariants is to describe this algebra. Thus, the invariants of forms are the invariants of the general linear group with respect to its representation in the space of symmetric tensors of fixed rank of the underlying (or dual) space (the coefficients of the original form $f$ are the components of this tensor); the consideration of covariants reduces to the study of the algebra of invariants for a representation in the space of tensors of mixed valency. In this form the problem of the description of invariants is a special case of the following general problem of the theory of linear representations: To decompose a space of tensors of given valency into irreducible invariant subspaces with respect to a given group of linear transformations of the underlying linear space (the search for invariants can be reduced to singling out the one-dimensional invariant subspaces).
Already at the first stages of development of the theory of invariants the following fact was discovered, which allowed one to consider the system of invariants as a whole: In all the cases examined it was possible to select a finite number of basic invariants $\phi _ { 1 } , \ldots , \phi _ { m }$, that is, invariants such that every other invariant $( 1 )$ of the given representation can be expressed as a polynomial in them: $\phi = F ( \phi _ { 1 } , \ldots , \phi _ { m } )$. In other words, the algebra of invariants proved to be finitely generated. It also became clear that these basic invariants are, in general, not independent (that is, the algebra of invariants is not a free algebra): there can exist non-trivial polynomials $P ( t _ { 1 } , \ldots , t _ { m } )$, called relations or syzygies, that after the substitutions $t _ { i } = \phi _ { i }$, $1 \leq i \leq m$, vanish identically. In the set of relations itself it is again possible to find a finite number of basic relations, all the remaining being algebraic consequences of them (the relations form an ideal in the ring of polynomials in the variables $t _ { 1 } , \ldots , t _ { m }$, and the basic relations are generators of it). In turn, the basic relations themselves are in general not independent; thus, secondary syzygies can be determined, etc. The chain of syzygies constructed in this way always turns out to be finite. For example, if $k$ is the symmetric group of all permutations of the coordinates $x _ { 1 } , \ldots , x _ { x }$, then the algebra of invariants is the algebra of all symmetric polynomials in $X _ { 1 } , \ldots , X _ { m }$; the elementary symmetric polynomials are basic invariants, which are algebraically independent (in this case there are no syzygies).
These facts led to the statement of two fundamental problems in the classical theory of invariants:
1) To prove that the algebra of invariants of a given representation of a given group is finitely generated (the first fundamental theorem of the theory of invariants) and to determine a system of basic invariants.
2) To prove the existence of a finite basis of syzygies (the second fundamental theorem of the theory of invariants) and to find it.
The first fundamental theorem of the theory of invariants for invariants of a form of arbitrary degree in an arbitrary finite number of variables was proved by D. Hilbert [1] (see also Hilbert theorem on invariants). He also proved that the second fundamental theorem of the theory of invariants is true in all those cases when the first fundamental theorem holds, and also that in this case the chain of syzygies is always finite. Hilbert obtained the proof of the fundamental theorems of the classical theory of invariants on the basis of general abstract algebraic results proved by him (with this specific aim). These results subsequently formed the foundation of modern commutative algebra (the Hilbert basis theorem, the Hilbert syzygies theorem, Hilbert's Nullstellensatz, cf. Hilbert theorem 1), 3) and 5)). The original proof of the first fundamental theorem of the theory of invariants was non-constructive and gave no upper estimate for the degree of basic invariants. In the 1930's H. Weyl, by developing an idea of Hilbert and A. Hurwitz [14], proved the first fundamental theorem of the theory of invariants for finite-dimensional representations of arbitrary compact Lie groups and for finite-dimensional representations of arbitrary complex semi-simple Lie groups [6]. The book [6], which summarizes the developments of the classical theory of invariants, contains a description of the basic invariants and syzygies for the representations of the classical groups as well as for certain other groups. One of the important applications of the methods of the theory of invariants was the description of the Betti numbers of classical compact groups.
The proof of the second fundamental theorem of the theory of invariants discloses the general algebraic nature of this theorem (it is a corollary of Hilbert's basis theorem). In attempting to determine whether this is also true with regard to the first fundamental theorem of the theory of invariants, Hilbert stated the following problem (Hilbert's 14th problem): Let $k$ be a field, let $A = k [ x _ { 1 } , \ldots , x _ { n } ]$ be the algebra of polynomials over $k$ in the variables $x _ { 1 } , \ldots , x _ { x }$ and let $L$ be an arbitrary subfield of the field of fractions of $4$ containing $k$. Is then the algebra $A \cap L$ finitely generated over $k$? An affirmative answer to this question would imply the validity of the first fundamental theorem of the theory of invariants for arbitrary groups. A negative solution to Hilbert's 14th problem was obtained in [9], in which an example was given of a representation of a commutative unipotent group for which the algebra of invariants does not have a finite number of generators. In the 1950's a number of results was obtained on invariants of finite groups, in particular groups generated by reflections (see Reflection group; Coxeter group). It has been proved [13], [14] that finite linear complex groups generated by unitary reflections can be characterized as the finite linear groups whose algebras of invariants do not contain syzygies.
A new stage of development of the theory of invariants was related to the extension of the circle of problems and to geometric applications of this theory. The modern theory of invariants (or the geometric theory of invariants) became a part of the general theory of algebraic transformation groups; the theory of algebraic groups constructed in 1950's is fundamental to it, and the language of algebraic geometry is fundamental to its language. In contrast with the classical theory of invariants, whose basic object was the ring of polynomials in $12$ variables over a field $k$ together with the group of automorphisms induced by linear changes of variables, the modern theory of invariants considers an arbitrary finitely-generated $k$-algebra $R$ and the algebraic group $k$ of its $k$-automorphisms. Instead of a linear space $V$ and a representation $0$, an arbitrary affine algebraic variety $x$ is considered together with the algebraic group $k$ of its algebraic transformations (automorphisms), such that $R$ is the ring of regular functions on $x$ and the action of $k$ on $R$ is induced by that of $k$ on $x$. The elements of $R$ that are fixed under $k$ are the invariants; the entire set of them forms a $k$-algebra, $R ^ { G }$.
Other notions of the classical theory of invariants can also be generalized. For example, the comitant, which is a regular mapping from one such variety into another commuting with the group action; if $R ^ { G }$ is finitely generated, then one says that the first fundamental theorem of the theory of invariants is valid. It has been proved that $R ^ { G }$ is finitely generated if $k$ is a geometrically-reductive group (see Mumford hypothesis). In many important cases, for example, in applications to the moduli problem, $k$ is in fact a group of this type. If $R ^ { G }$ is finitely generated, then there exists an affine algebraic variety $v$ for which $R ^ { G }$ is the algebra of regular functions; the imbedding $R ^ { G } \subset R$ induces a morphism $\pi : X \rightarrow W$. If $k$ is geometrically reductive, then $v$ classifies the closed orbits of $k$ in $v$: $31$ is surjective and in each of its fibres there is exactly one closed orbit. A necessary condition for the existence of a quotient variety of $x$ with respect to $k$, which is that all the orbits be closed, turns out to be sufficient also, and $v$ proves to be this quotient variety. Hence the role of $R ^ { G }$ in the solution of the geometric problems of classifying and constructing quotient varieties becomes clear; apart from this, the study of $R ^ { G }$ (which was the final aim of the classical theory of invariants) is only the beginning stage for the solution of these geometric problems, since knowledge of $R ^ { G }$ does not, in general, provide complete information on the orbits of $k$ in $x$ and must therefore be combined with the consideration of non-closed orbits, their closures and stabilizers (so-called orbital decompositions). Furthermore, the study of actions of algebraic groups on affine algebraic varieties is only the "local part" of the general theory of algebraic transformation groups (just as the theory of affine varieties is the "local part" of the general theory of algebraic varieties).
In the general case one considers an algebraic (regular) action of $k$ on an arbitrary algebraic variety $x$ (glued together from affine pieces), so that, e.g., the solution of the problem of constructing a quotient variety of $x$ (or of a suitable open subset of $x$) with respect to the action of $k$ reduces to the consideration of a $k$-invariant affine covering of $x$ and the application of the above construction to each element of this covering with subsequent "glueing" of the affine quotient varieties obtained. For a successful application of the procedure, $x$ must, in general, be replaced by some invariant subset of it ($x$ itself need not have an invariant affine covering).
At present, investigations on the theory of algebraic transformation groups are conducted in various directions, from which one can select the following: To obtain information on the properties of points in general position on a variety $x$ on which an algebraic group $k$ acts regularly; to describe the orbital decompositions of various specific actions (mainly linear representations); theorems on stratification of general spaces of transformations into simpler standard spaces; theorems on quotient varieties, orbit spaces, spaces of sections, quasi-sections and "slices" , as well as on varieties of fixed points; theorems on equivalent imbeddings; criteria for the affineness and quasi-affineness of orbits (see Matsushima criterion); the structure of the closure of orbits of various special types, the theory of quasi-homogeneous varieties (that is, varieties with a dense orbit) and the theory of actions with a trivial algebra of invariants; the algebraic properties of rings of invariants, the algebraic-geometric properties of spaces of transformations of quotient varieties; the connection with the theory of singularities [16]); the problem of the rationality of fields of invariants, and the connection with the theory of algebraic tori and algebraic number theory [17]).
References
| [1] | D. Hilbert, "Ueber die Theorie der algebraischen Formen" Math. Ann. , 36 (1890) pp. 473–534 MR1510634 Zbl 22.0133.01 |
| [2] | D. Hilbert, "Ueber die vollen Invariantensysteme" Math. Ann. , 42 (1893) pp. 313–373 MR1510781 Zbl 25.0173.01 |
| [3] | R. Weitzenböck, "Invarianten Theorie" , Noordhoff (1923) Zbl 0014.10101 Zbl 62.0074.01 |
| [4] | A. Hurwitz, "Ueber die Erzeugung von Invarianten durch Integration" Gött. Nachr. (1897) pp. 71–90 |
| [5] | F. Klein, "Development of mathematics in the 19th century" , Math. Sci. Press (1979) pp. Chapt. 1 (Translated from German) MR0529278 MR0549187 Zbl 0411.01009 |
| [6] | G.B. Gurevich, "Algebraic theory of invariants" , Noordhoff (1964) (Translated from Russian) Zbl 0128.24601 |
| [7] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [8] | "Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [9] | M. Nagata, "On the fourteenth problem of Hilbert" J.A. Todd (ed.) , Proc. Internat. Congress Mathematicians (Edinburgh, 1958) , Cambridge Univ. Press (1960) pp. 459–462 MR0116056 Zbl 0127.26302 |
| [10] | M. Nagata, "On the 14-th problem of Hilbert" Amer. J. Math. , 81 (1959) pp. 766–772 MR0105409 Zbl 0192.13801 |
| [11] | D. Mumford, "Geometric invariant theory" , Springer (1965) MR0214602 Zbl 0147.39304 |
| [12] | J. Dieudonné, J.B. Carrell, "Invariant theory: old and new" , Acad. Press (1971) MR0279102 Zbl 0258.14011 |
| [13] | S. Fogarty, "Invariant theory" , Benjamin (1969) MR0240104 Zbl 0191.51701 |
| [14] | C. Chevalley, "Invariants of finite groups generated by reflections" Amer. J. Math. , 77 (1955) pp. 778–782 MR0072877 Zbl 0065.26103 |
| [15] | G.C. Shephard, J.A. Todd, "Finite unitary reflection groups" Canad. J. Math. , 6 (1954) pp. 274–304 MR0059914 Zbl 0055.14305 |
| [16] | P. Wagreich, "Algebraic varieties with group action" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1975) pp. 633–642 MR0382264 Zbl 0321.14025 |
| [17] | V.E. Voskresenskii, "Fields of invariants for Abelian groups" Russian Math. Surveys , 28 : 4 (1972) pp. 79–105 Uspekhi Mat. Nauk , 28 : 4 (1972) pp. 77–102 Zbl 0289.14006 |
Comments
References
| [a1] | T.A. Springer, "Invariant theory" , Lect. notes in math. , 585 , Springer (1977) MR0447428 Zbl 0346.20020 |
| [a2] | D. Mumford, "Hilbert's fourteenth problem - the finite generation of subrings such as rings of invariants" F.E. Browder (ed.) , Mathematical developments arising from Hilbert problems , Proc. Symp. Pure Math. , 28 , Amer. Math. Soc. (1976) pp. 431–444 MR435076 |
Maximilian Janisch/latexlist/Algebraic Groups/Invariants, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Invariants,_theory_of&oldid=44014