User:Maximilian Janisch/latexlist/Algebraic Groups/Differential algebra

This page is a copy of the article Differential algebra in order to test automatic LaTeXification. This article is not my work.

A branch of algebra which deals with objects which involve not only addition and multiplication operations but also the operation of differentiation: differential rings, differential modules, differential fields, and differential algebraic varieties.

One of the main objects of differential algebra is the algebra of differential polynomials $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$, which is the analogue of the ring of polynomials in commutative algebra (cf. Extension of a differential field). Each system of differential equations

\begin{equation} F _ { 1 } = 0 , \ldots , F _ { k } = 0 \end{equation}

corresponds to the perfect differential ideal $\{ F _ { 1 } , \ldots , F _ { k } \}$ generated by this system in the algebra of differential polynomials. The Ritt–Raudenbush basis theorem states that all perfect differential ideals are obtained in this way (a differential ideal $1$ is called perfect if whenever $a ^ { N } \in I$ for some $n > 0$, then $\alpha \in I$), i.e. it is possible to select in any such ideal a finite number of differential polynomials such that the perfect differential ideal generated by these polynomials corresponds to the given ideal. As distinct from Hilbert's basis theorem in a polynomial ring, the essential feature of the Ritt–Raudenbush theorem is that the ideals are perfect, i.e. differential ideals (even perfect differential ideals) need not be finitely-generated differential modules.

A perfect differential ideal corresponds to a differential algebraic variety — the set of points in an affine space over some universal extension of the field of coefficients on which any polynomial from this ideal vanishes. The analogue of Hilbert's Nullstellensatz is valid. Let $F _ { 1 } , \ldots , F _ { p }$ be a finite system of differential polynomials and let $k$ be a differential polynomial which vanishes in all solutions of this system. A certain power of $k$ will then be a linear combination of the $F$ and their derivatives of various orders with coefficients from the algebra of differential polynomials. In particular, if the system $F _ { 1 } , \ldots , F _ { p }$ has no zeros, then some linear combination of the $F$ and their derivatives of various orders will be equal to one.

A perfect differential ideal may be represented as the intersection of a finite number of prime differential ideals. To such a representation corresponds the decomposition of a variety into a finite number of irreducible components. As in algebraic geometry, the concept of a generic zero and its dimension is introduced for prime differential ideals. For an irreducible closed set $V$ in a differential affine space, i.e. in an affine space over a universal extension $r$ of the field of coefficients, one defines a differential dimension polynomial

\begin{equation} \omega _ { V } = \sum _ { 0 \leq i \leq m } \alpha _ { i } \left( \begin{array} { c } { x + i } \\ { i } \end{array} \right) \end{equation}

where $m$ is the number of differentiations in $H ^ { \prime }$. The coefficient $a _ { n }$ is known as the differential dimension of $V$, the degree $\tau = \operatorname { deg } \omega _ { V }$ of the polynomial is known as the differential type of the set $V$, while the coefficient $a _ { \tau }$ is called its typical differential dimension. The polynomial $C$ is a birational invariant, but is not a differential birational invariant. This is the case for $( V )$, $\tau ( V )$ and $a _ { \tau \langle V \rangle } ( V )$. The determination of differential birational invariants is of major interest. Another problem is to estimate the possible values of the invariants obtained. Let $2$ be a set in $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$. If the orders of the elements of $2$ are bounded, then the differential dimension polynomials of the components of $\{ \sum \}$ are subject to certain restrictions. In particular, if for each $Y$ the order of any element of $2$ with respect to $Y$ does not exceed $e$, it follows from the condition $\alpha _ { m } ( p ) = 0$ that, for any component of the variety $\{ \sum \}$, one has $a _ { m - 1 } ( p ) \leq \sum e _ { j }$. The hypothesis in the general case is

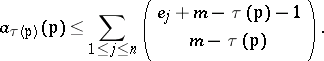This hypothesis is not valid, as was shown by M. Kondrat'eva. If the set $\Sigma \subset F \{ Y _ { 1 } , \ldots , Y _ { N } \}$ consists of $12$ differential polynomials $F _ { 1 } , \ldots , F _ { n }$, two additional hypotheses are also postulated. Let

\begin{equation} e _ { i j } = \operatorname { ord } _ { Y } _ { j } F _ { i } , \quad 1 \leq i \leq n , \quad i \leq j \leq n \end{equation}

and

\begin{equation} h = \operatorname { max } _ { \pi } ( e _ { 1 } \pi ( 1 ) + \ldots + e _ { n } \pi ( n ) ) \end{equation}

where $31$ runs through the symmetric group $S _ { n }$. The first hypothesis states that for any component $D$ of the variety $\{ F _ { 1 } , \ldots , F _ { x } \}$ it follows from $\alpha _ { m } ( p ) = 0$ that $a _ { m - 1 } ( p ) \leq h$. This statement has been proved in a number of special cases. According to the second hypothesis, for any component $D$ of the variety $\{ F _ { 1 } , \ldots , F _ { x } \}$ it follows from 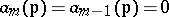that $\omega _ { p } = 0$. This hypothesis has been proved.

A difficult problem in differential algebra is the decomposition of a differential algebraic variety into irreducible components. Even if $2$ consists of a single irreducible differential polynomial $\Omega$ the corresponding variety usually consists of several components, one of which contains all non-singular solutions of the equation $\sigma = 0$ (and may also contain singular solutions), while all the remaining components consist of solutions in which any separant of the differential polynomial $\Omega$ vanishes. The case of a hypersurface (a system $2$ of one equation) is especially important, since any differential algebraic variety over an ordinary differential field is differentially birationally isomorphic to a hypersurface.

Since any prime differential ideal is completely defined by its characteristic set, one may subdivide the problem of the decomposition of a differential algebraic variety $\{ p \}$ into two parts: 1) to find a finite set $t$ of autoreduced subsets of $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$ each of which is a characteristic set of a prime differential ideal containing $\Phi$ such that $t$ contains a characteristic set of each component of $\{ \Phi \}$; 2) to determine, for a given autoreduced set in $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$ whether or not it is a characteristic set of any component of $\{ \Phi \}$.

The solution of 2) is not known (1987) in the general case, but the important special case when $\Phi$ consists of one differential polynomial can be solved with the aid of two theorems of Ritt: The component theorem and the low power theorem (see below).

The problem of finding the components of the variety $\{ \Phi \}$ may also be decomposed into problem 1) and the following problem: 3) to determine, for given characteristic sets $4$ and $B$ of prime differential ideals $D$ and $q$ respectively, if the inclusion $p \subset q$ holds.

Problem 3) is also still far from being solved. In the particular case when $4$ consists of one irreducible differential polynomial $4$ and $q$ is a differential ideal $[ Y _ { 1 } , \ldots , Y _ { n } ]$, the problem is to find whether or not the point $( 0 , \ldots , 0 )$ is comprised in the general solution of the differential equation $A = 0$.

Problem 1) has been solved, "in principle" , for a finite set $\Phi \subset F \{ Y _ { 1 } , \ldots , Y _ { N } \}$: An inductive procedure (the theory of elimination for systems of algebraic differential equations) converts it to a number of "easier" problems involving polynomials in a finite number of unknowns over $F$, i.e. a problem involving algebraic differential equations is reduced to one involving algebraic equations.

The components theorem says that the singular components are in their turn generic components of other differential polynomials. More exactly, let $F$ be a differential field and let $H ^ { \prime }$ denote a non-zero differential polynomial in $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$. If $D$ is some component of the ideal $\{ F \}$ of the ring $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$, then there exists an irreducible differential polynomial $B \in F \{ Y _ { 1 } , \ldots , Y _ { N } \}$ such that $p = p _ { F } ( B )$ is a generic component of the variety $\{ B \}$.

The low power theorem provides a criterion for determining whether or not the component of an irreducible differential polynomial $A \in F \{ Y _ { 1 } , \ldots , Y _ { N } \}$ is a component of $\{ F \}$. More exactly, let $F , A \in F \{ Y _ { 1 } , \ldots , Y _ { n } \}$, let the orders of $H ^ { \prime }$ and $4$ with respect to $Y _ { n }$ be equal to $m$ and $1$, respectively, let $A _ { j }$ be the $i$-th derivative of $4$ and let $5$ be the separant of $4$. There exist a $t \geq 0$ and an $r > 0$ such that

\begin{equation} S ^ { t } F = \sum _ { j = 1 } ^ { r } c _ { j } A ^ { p _ { j } } A _ { 1 } ^ { i _ { 1 j } } \dots A _ { m - l } ^ { i _ { m - l } , j } \end{equation}

where $p _ { j } \geq 0$, $\dot { w } _ { k j } \geq 0$, no two sets coincide, the order of $C$ with respect to $Y _ { n }$ does not exceed $1$, and $C$ is not divisible by $4$. If such a decomposition has been found, the low power theorem states that a generic component of the variety $\{ A \}$ is a component of the variety $\{ F \}$ if and only if the decomposition, when written out, contains a term $c _ { k } A ^ { p } k$ which does not contain derivatives of $4$ and the degree of which is lower than the degree of any other term in the decomposition, regarded as a polynomial in $A _ { 1 } , \ldots , A _ { m } - l$ (if the characteristic is non-zero, this condition is neither necessary nor sufficient).

The second trend of studies in differential algebra concerns the problem of extensions of specializations. Let $( \eta _ { 1 } , \ldots , \eta _ { n } )$ and $( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ be points in $U ^ { N }$, where $r$ is a universal extension of a differential field $F$. A point $( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ is said to be a differential specialization of the point $( \eta _ { 1 } , \ldots , \eta _ { n } )$ over $F$ (this is denoted by $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$) if any differential polynomial which vanishes in $( \eta _ { 1 } , \ldots , \eta _ { n } )$ also vanishes in $( \zeta _ { 1 } , \ldots , \zeta _ { n } )$. If $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ and $1 \leq k \leq n$, it is clear that $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$. One says that the first specialization is an extension of the second.

Let $( \eta _ { 1 } , \ldots , \eta _ { n } )$ and $k$ be given, and let $B \in F \{ Y _ { 1 } , \ldots , Y _ { N } \}$ be such that $B ( \eta _ { 1 } , \ldots , \eta _ { n } ) \neq 0$. It can be shown that there exists a non-zero differential polynomial $B _ { 0 } \in F \{ Y _ { 1 } , \ldots , Y _ { k } \}$ satisfying the condition $B _ { 0 } ( \eta _ { 1 } , \ldots , \eta _ { k } ) \neq 0$ such that any differential specialization $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ for which $B _ { 0 } ( \zeta _ { 1 } , \ldots , \zeta _ { k } ) \neq 0$ may be extended to a differential specialization $( \zeta _ { 1 } , \ldots , \zeta _ { n } )$ where $B ( \zeta _ { 1 } , \ldots , \zeta _ { n } ) \neq 0$. However, unlike the situation in algebraic geometry, a differential specialization $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ cannot always be extended to a differential specialization $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$, even if the elements $\zeta _ { k + 1 } , \ldots , \zeta _ { x }$ assume the value $\infty$. Thus, the resulting problem is to find a criterion for the possibility of an extension of a specialization $( \eta _ { 1 } , \ldots , \eta _ { k } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { k } )$ to a differential specialization $( \eta _ { 1 } , \ldots , \eta _ { n } ) \rightarrow F ( \zeta _ { 1 } , \ldots , \zeta _ { n } )$.

A special case of this problem is encountered in the problem of indeterminate forms. Let the polynomials $F , G \in F \{ Y _ { 1 } , \ldots , Y _ { n } \}$ be relatively prime, let $G \neq 0$, and let $H ^ { \prime }$ and $k$ vanish at $( 0 , \ldots , 0 )$. The problem is to assign to the ratio $F / G$ a value at the point $( 0 , \ldots , 0 )$. Let the elements $t _ { 1 } , \ldots , t _ { x } \in U$ be differentially algebraically independent over $F$ and let

\begin{equation} u = \frac { F ( t _ { 1 } , \ldots , t _ { x } ) } { G ( t _ { 1 } , \ldots , t _ { x } ) } \end{equation}

It is natural to say that $F / G$ admits the value $6$ at $( 0 , \ldots , 0 )$ if $( t _ { 1 } , \ldots , t _ { n } , u ) \rightarrow F ( 0 , \ldots , 0 , \alpha )$. Thus, the problem is reduced to finding the extensions of $( t _ { 1 } , \ldots , t _ { n } ) \rightarrow F ( 0 , \ldots , 0 )$ to $( t _ { 1 } , \ldots , t _ { x } , u )$. This is equivalent to determining the elements $\alpha \in U$ such that $( 0 , \ldots , 0 , \alpha )$ is a zero of the generic component of the differential polynomial $Y _ { n + 1 } G - F \in F \{ Y _ { 1 } , \ldots , Y _ { n + 1 } \}$. J.F. Ritt conjectured that $6$ is either uniquely defined (possibly equal to $\infty$) or else is completely arbitrary; he proved this conjecture for ordinary differential fields for $n = 1$, $d ( F G ) = 1$. Studies are made of the properties of concrete differential ideals in the ring $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$. In the case of an infinite sequence $\Sigma _ { 1 } , \ldots , \sum _ { p } , \ldots ,$ of prime differential ideals in $F \{ Y _ { 1 } , \ldots , Y _ { n } \}$, where each $\Sigma$ is a proper divisor of $\Sigma _ { i + 1 }$, the intersection of all $\Sigma$ is a prime differential ideal and the dimension of the corresponding variety $M$ is higher than that of the variety $M$ corresponding to $\Sigma$ for an arbitrary $i$.

Of the other results concerning differential algebraic varieties, the analogue of Lüroth's theorem is worth mentioning: If $G$ is an extension of a differential field $F$ contained in $F \{ u \}$, then $G$ contains an element $v$ such that $F ( v ) = G$.

However, the theory of differential algebraic curves (varieties of differential dimension 1) is only in its initial stage of development; even for invariants such as the genus of the curve in algebraic geometry, differential algebraic analogues have not been found. Of major interest is the intersection theory of differential algebraic varieties. The theorem that the intersection of two irreducible varieties of dimensions $D$ and $h$ in $12$-dimensional affine space has dimension $p + q - n$ or higher is not valid for these varieties. However, differential algebraic varieties are characterized not only by the dimension but also by their order with respect to a chosen differential transcendence basis. A number of estimates from above have been obtained for the intersection order of varieties with respect to a specially chosen basis. The following analytic theorem on the intersection of components of the same differential polynomial has been proved: If $H ^ { \prime }$ is a differential polynomial in the unknowns $Y _ { 1 } , \ldots , Y _ { n }$, then in a zero of the polynomial $H ^ { \prime }$ contained in more than one component of $H ^ { \prime }$ the derivative $\partial F / \partial Y _ { i j }$ vanishes for $i = 1 , \dots , n$ and arbitrary $i$. The concept of a differential algebraic variety may be generalized (dropping the assumption that it is affine). In particular, it is possible to introduce the concepts of differentially homogeneous polynomials and of projective differential algebraic varieties.

For a differential field $H ^ { \prime }$ there is no differential algebraic closure, and differential algebraically closed fields do not exist. They are replaced, in a sense, by the so-called "constrained" extensions.

The Galois theory of differential fields represents a trend in differential algebra. A universal differential extension $r$ of a differential field $F$ is constructed and the set of differential isomorphisms from a finitely-generated differential algebraic extension $G$ of the field $F$ into $r$ which are the identity on $F$ are considered. If $G$ is a strongly normal extension of $F$, it is possible to introduce the structure of an algebraic group over the field $K$ (of constants of $r$) on the set $k$ of differential isomorphisms from $G$ into $r$. A special case of strongly normal extensions are the Picard–Vessiot extensions, obtained by adding to the field $F$ the solutions of a linear homogeneous differential equation with coefficients in $F$. The Galois group of a Picard–Vessiot extension is an algebraic matrix group. The correspondence between the intermediate fields and the subgroups of the group $k$ is described by the following theorem.

Let $G$ be a strongly normal extension of a differential field $F$ with field of constants $C$. a) If $F _ { 1 }$ is a differential field such that $F \subset F _ { 1 } \subset G$, then $G$ is strongly normal over $F _ { 1 }$, the Galois group $G ( G / F _ { 1 } )$ is a $C$-subgroup in $G ( G / F )$ and the field of invariants of $G ( G / F _ { 1 } )$ in $G$ coincides with $F _ { 1 }$. b) If $G$ is a $C$-subgroup of $G ( G / F )$ and $F _ { 1 }$ denotes the set of invariants of the group $G$ in $G$, then $F _ { 1 }$ is a differential field, $F \subset F _ { 1 } \subset G$ and $G ( G / F _ { 1 } ) = G _ { 1 }$.

The normal subgroups $G$ of $G ( G / F _ { 1 } )$ correspond to strongly normal extensions $F _ { 1 }$ of $F$ and vice versa. The inverse Galois problem — that is, the problem of the existence of a strongly normal extension $G$ of a field $F$ the Galois group $G ( G / F )$ of which is isomorphic to a given group — has been solved for connected solvable groups. The problem was reduced to an estimate of the dimension of some vector space over the field of constants $C$ of $F$ and the rank of a certain Abelian group. Results on the Galois theory of infinite extensions are available. The theory of integration in finite form deals with problems related to Galois theory.

The theory of differential algebraic groups, substantially different from its algebraic analogue, is in the course of development. In particular, the differential ring of everywhere-defined differential rational functions on an affine differential algebraic set is not a differential coordinate ring and, in general, is not finitely generated as a differential algebra.

The analogue of Liouville's theorem on the approximation of algebraic numbers by rational numbers may be mentioned as a result obtained for the approximation of differential algebraic functions by differential rational functions. However, the analogue of the Thue–Siegel–Roth theorem has not yet (1987) been proved.

The theory of rings with higher differentiations is now being developed. Higher differentiations are a strong tool in the study of objects of non-zero characteristic. If the characteristic of the differential ring $4$ is $D$, the $D$-th power of any element is constant; this is not true of rings with higher differentiations. Analogues of many results listed above, concerning both the intersection theory of ideals and Galois theory, have been obtained for rings with higher differentiations.

References

[1]	I. Kaplansky, "An introduction to differential algebra" , Hermann (1957) MR0093654 Zbl 0083.03301
[2]	J.F. Ritt, "Differential algebra" , Amer. Math. Soc. (1950) MR0035763 Zbl 0037.18402
[3]	E.R. Kolchin, "Differential algebra and algebraic groups" , Acad. Press (1973) MR0568864 Zbl 0264.12102
[4]	E.R. Kolchin, "Some problems in differential algebra" , Proc. Internat. Congress Mathematicians (Moscow, 1966) , Mir (1968) pp. 269–276 MR0237476 Zbl 0197.31601

Comments

For the notion of dimension polynomial of an extension of differential fields cf. Dimension polynomial. Universal extensions of a differential field, a substitute for the algebraic geometric notion of a universal (i.e. large enough algebraically closed) extension of the base field $k$ one is working over, are discussed in Extension of a differential field. The various other notions of differential algebra which occur in the main article above are described below.

Let $R = ( R , \partial _ { 1 } , \ldots , \partial _ { m } )$ be a differential ring consisting of the commutative ring with unit element $R$ and the commuting derivations $\partial _ { i } : R \rightarrow R$, $i = 1 , \ldots , m$. A differential ideal of $P$ is an ideal $\pi$ of $R$ such that $\partial _ { i } I \subset I$ for all $i$. Let $( n$ denote the free commutative semi-group generated by the $0$, $i = 1 , \ldots , m$. The elements of $( n$ are called the derivative operators of $P$. If $\theta = \Pi _ { i } \partial _ { i } ^ { e _ { i } ^ { e _ { i } } }$, the order of $6$ is $\operatorname { ord } ( \theta ) = \sum e$.

Now consider a set $\{ y _ { 1 } , \ldots , y _ { n } \}$ of differential indeterminates over $P$ (i.e. the $y _ { 1 } , \ldots , y _ { x }$ are differentiably algebraically independent over $P$, cf. Extension of a differential field). A ranking of $\{ y _ { 1 } , \ldots , y _ { n } \}$ is a total order on the set of all derivatives $\theta y _ { 2 }$, $\theta \in \Theta$, that satisfies for all such derivatives $u _ { 3 }$ the conditions: $u \leq \theta u$ and $u \leq v \Rightarrow \theta u \leq \theta v$, for all $\theta \in \Theta$. Let $A \in R \{ y _ { 1 } , \ldots , y _ { n } \}$, the ring of differential polynomials in $y _ { 1 } , \ldots , y _ { x }$ over $P$. The highest ranking derivative $\theta y _ { 2 }$ present in $4$ is called the leader of the differential polynomial $4$; it will be denoted by $u _ { A }$. Let $d = d e g _ { A } ( A )$, then $4$ can be written in the form $A = \sum _ { i = 0 } ^ { d } A _ { i } u _ { A } ^ { i }$ where the $A$ are in $R \{ y _ { 1 } , \ldots , y _ { n } \}$ and do not contain $u _ { A }$ (or any higher ranking derivative). The differential polynomial $A _ { d }$ is called the initial differential polynomial of $4$ and the differential polynomial $\sum i A u _ { A } ^ { i - 1 }$ ($= \partial A / \partial u _ { A }$) is called the separant of $4$. All these notions are dependent on the ranking used. It is useful to extent the total order on the $\theta y _ { 2 }$ to a comparative rank on all elements of $R \{ y _ { 1 } , \ldots , y _ { n } \}$. This is done as follows.

a) Every element of $P$ has lower rank than every element of $R \{ y _ { 1 } , \ldots , y _ { N } \} \backslash R$.

b) Let $B \in R \{ y _ { 1 } , \ldots , y _ { x } \} \backslash R$. If $u _ { A } < x$ (or $u _ { A } = u _ { B }$ and $\operatorname { deg } _ { A } ( A ) < \operatorname { deg } _ { A } ( B )$), then $A \leq B$.

c) All elements in $P$ have the same rank.

d) If $u _ { A } = u _ { B }$ and $\operatorname { deg } _ { A } ( A ) = \operatorname { deg } _ { A } ( B )$, then $4$ and $B$ have the same rank. Different differential polynomials may of course have the same rank but this does define in any case a partial order on $R \{ y _ { 1 } , \ldots , y _ { n } \}$.

Let $A \in R \{ y _ { 1 } , \ldots , y _ { n } \} \backslash R$ and let $F \in R \{ y _ { 1 } , \ldots , y _ { n } \}$. The differential polynomial $H ^ { \prime }$ is called partially reduced with respect to $4$ if $H ^ { \prime }$ contains no proper derivative of $u _ { A }$ (i.e. contains no $\theta u _ { A }$, $\theta \in \Theta$). If, moreover, $\operatorname { deg } _ { A } ( F ) < \operatorname { deg } _ { A } ( A )$, $H ^ { \prime }$ is said to be reduced with respect to $4$. More generally, $H ^ { \prime }$ is said to be reduced with respect to a subset $\Sigma \subset R \{ y _ { 1 } , \ldots , y _ { n } \} \backslash R$ if $H ^ { \prime }$ is reduced with respect to every member of $2$. A subset $2$ of $R \{ y _ { 1 } , \ldots , y _ { n } \}$ is said to be autoreduced if $\Sigma \cap R = \emptyset$ and if each element $H ^ { \prime }$ of $2$ is reduced with respect to $\Sigma \backslash \{ F \}$. Every autoreduced set is finite. These sets were introduced by Ritt (who called them ascending sets or chains) as a tool in his process of reduction of differential polynomials. This process plays a role analogous to Euclidean division (with remainder) for ordinary polynomials.

The notion of comparative rank of elements of $R \{ y _ { 1 } , \ldots , y _ { n } \}$ is extended to a ranking of autoreduced subsets of $R \{ y _ { 1 } , \ldots , y _ { n } \}$ as follows. Let $A = \{ A _ { 1 } , \ldots , A _ { \cdot } \}$ and $B = \{ B _ { 1 } , \ldots , B _ { s } \}$ be autoreduced subsets of $R \{ y _ { 1 } , \ldots , y _ { n } \}$, where both $A _ { 1 } , \ldots , A _ { r }$ and $B _ { 1 } , \ldots , B _ { s }$ are arranged in orders of increasing rank.

e) If there exists a $k \in N = \{ 1,2 , \ldots \}$, $k \leq \operatorname { min } ( r , s )$, such that $\operatorname { rank } ( A _ { i } ) = \operatorname { rank } ( B _ { i } )$, $i < k$ and $( A _ { k } ) < \operatorname { rank } ( B _ { k } )$, then $t$ has lower rank than $8$.

f) If $r > s$ and $\operatorname { rank } ( A _ { i } ) = \operatorname { rank } ( B _ { i } )$, $i = 1 , \dots , s$, then $t$ has lower rank than $8$.

g) If $r = S$ and $\operatorname { rank } ( A _ { i } ) = \operatorname { rank } ( B _ { i } )$, $i$, then $t$ and $8$ have the same rank.

Now let $\pi$ be a differential ideal in $R \{ y _ { 1 } , \ldots , y _ { n } \}$. Then there exists an autoreduced set $A \subset I$ such that the separant $S _ { A }$ of $4$ is not in $\pi$ for all $A \in A$. Such an autoreduced subset of lowest rank of $\pi$ is called a characteristic set of $\pi$.

Consider again a differential polynomial $A \in R \{ y _ { 1 } , \ldots , y _ { n } \}$. If there is a $u = \theta y _ { i }$, $\theta \in \Theta$, such that $\partial A / \partial u \neq 0$, then there is such a $21$ of maximal order. This order is called the essential order of $4$. There is then also such a $v$ (such that $\partial A / \partial v \neq 0$) of highest rank. If, moreover, $4$ does not contain any proper derivative of $v$, then $v$ is called the pseudo-leader of $4$ (relative to the given ranking); the pseudo-separant of $4$ is then $\partial A / \partial v$. (If $k a \neq 0$ for all $k \in N$, $0 \neq \alpha \in R$, then the notions of pseudo-leader and pseudo-separant of course coincide with those of leader and separant, but if $P$ is of characteristic $p \neq 0$, e.g., this need not be the case.)

Let $21$ be a universal extension of $k \{ y _ { 1 } , \ldots , y _ { n } \}$, where $k$ is a differential field. Let $A \in k \{ y _ { 1 } , \dots , y _ { n } \}$. A point $\eta \in U ^ { x }$ is called a non-singular zero of $4$, or a non-singular solution of $A = 0$, if $7$ is a zero of $4$ and there exists a ranking of $\{ y _ { 1 } , \ldots , y _ { n } \}$ relative to which $4$ is pseudo-led and such that the corresponding pseudo-separant does not vanish at $7$. The order zeros of $4$ (solutions of $A = 0$) are called singular zeros (singular solutions).