User:Maximilian Janisch/latexlist/Algebraic Groups/Contragredient representation

This page is a copy of the article Contragredient representation in order to test automatic LaTeXification. This article is not my work.

to a representation $( 1 )$ of a group $k$ in a linear space $V$

The representation $\phi ^ { * }$ of the same group $k$ in the dual space $V ^ { * }$ of $V$ defined by the rule

\begin{equation} \phi ^ { * } ( g ) = \phi ( g ^ { - 1 } ) ^ { * } \end{equation}

for all $g \in G$, where $3 + 5$ denotes taking adjoints.

More generally, if $v$ is a linear space over the same field $k$ as $V$ and $( , )$ is a non-degenerate bilinear form (pairing) on $V \times W$ with values in $k$, then a representation $25$ of $k$ in $v$ is called the representation contragredient to $( 1 )$ with respect to the form $( , )$ if

\begin{equation} ( \phi ( g ) x , y ) = ( x , \psi ( g ^ { - 1 } ) y ) \end{equation}

for all $g \in G$, $x \in V$, $y \in W$.

For example, if $k$ is the general linear group of a finite-dimensional space $V$, then the natural representation of $k$ in the space of covariant tensors of fixed rank on $V$ is the representation contragredient to the natural representation of $k$ in the space of contravariant tensors of the same rank on $V$.

Let $V$ be finite-dimensional over $k$, let $( e )$ be a basis of it, and let $( f )$ be the basis dual to $( e )$ in $V ^ { * }$. Then, for any 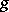in $k$, the matrix of $\phi ^ { * } ( g )$ in the basis $( f )$ is obtained from the matrix of the operator $\phi ( g )$ in the basis $( e )$ by taking the transpose of the inverse. If $( 1 )$ is irreducible, then so is $\phi ^ { * }$. If $k$ is a Lie group with Lie algebra $8$, and $d \phi$ and $d \psi$ are the representations of the algebra $8$ induced, respectively, by two representations $( 1 )$ and $25$ of $k$ in spaces $V$ and $v$ that are contragredient with respect to the pairing $( , )$, then

\begin{equation} ( d \phi ( X ) ( x ) , y ) = - ( x , d \psi ( X ) y ) \end{equation}

for all $X \in g$, $x \in V$, $y \in W$. Representations of a Lie algebra $8$ satisfying the condition (*) are also called contragredient representations with respect to $( , )$.

Suppose further that $k$ is a complex, connected, simply-connected semi-simple Lie group and that $( 1 )$ is an irreducible finite-dimensional representation of it in a linear space $V$. The weights of the representation $\phi ^ { * }$ are opposite to those of $( 1 )$ (see Weight of a representation of a Lie algebra), the lowest weight of $\phi ^ { * }$ being opposite to the highest weight of $( 1 )$ (see Cartan theorem on the highest (weight) vector). The representations $( 1 )$ and $\phi ^ { * }$ are equivalent if and only if there is a non-zero bilinear form on $V$ that is invariant with respect to $\phi ( G )$. If such a form exists, then it is non-degenerate and either symmetric or skew-symmetric. The set of numerical marks of the highest weight of the representation $\phi ^ { * }$ is obtained from the set of numerical marks of $( 1 )$ by applying the substitution induced by the following automorphism $2$ of the Dynkin diagram of simple roots $\Delta$ of $k$:

a) $2$ takes each connected component $\Delta _ { j }$, $i = 1 , \ldots , l$, of $\Delta$ into itself;

b) if $\Delta _ { j }$ is a diagram of type $A$, $D _ { 2 r + 1 }$ or $E _ { 0 }$, then the restriction of $2$ to $\Delta _ { j }$ is uniquely defined as the unique element of order 2 in the automorphism group of $\Delta _ { j }$; in the remaining cases the restriction of $2$ to $\Delta _ { j }$ is the identity.

References

[1]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian) MR0793377 Zbl 0484.22018
[2]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) MR0412321 Zbl 0342.22001
[3]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013
[4]	E.B. Vinberg, A.L. Onishchik, "Seminar on algebraic groups and Lie groups 1967/68" , Springer (Forthcoming) (Translated from Russian)

Comments

If $\Lambda \in \mathfrak { g } ^ { * }$ is the highest weight of the highest weight representation $( 1 )$, then the set of numerical marks of $1$ is simply the ordered set of integers $( k _ { 1 } , \ldots , k _ { r } )$, $k _ { i } = \Lambda ( h _ { i } )$; cf. Cartan theorem, especially when written as labels at the corresponding nodes of the Dynkin diagram.