User:Maximilian Janisch/latexlist/Algebraic Groups/Cartan subalgebra
of a finite-dimensional Lie algebra $8$ over a field $k$
A nilpotent subalgebra of $8$ which is equal to its normalizer in $8$. For example, if $8$ is the Lie algebra of all complex square matrices of a fixed order, then the subalgebra of all diagonal matrices is a Cartan subalgebra in $8$. A Cartan subalgebra can also be defined as a nilpotent subalgebra $1$ in $8$ which is equal to its Fitting null-component (cf. Weight of a representation of a Lie algebra)
\begin{equation} \mathfrak { g } 0 = \{ X \in \mathfrak { g } : \forall H \in \mathfrak { t } \exists \mathfrak { n } X , H \in Z ( ( \text { ad } H ) ^ { n } X , H ( X ) = 0 ) \} \end{equation}
where $a d$ denotes the adjoint representation (cf. Lie algebra) of $8$.
Suppose further that $k$ is of characteristic zero. Then for any regular element $x \in \mathfrak { Q }$, the set $n ( X , g )$ of all elements of $8$ which are annihilated by powers of $\operatorname { ad } X$ is a Cartan subalgebra of $8$, and every Cartan subalgebra of $8$ has the form $n ( X , g )$ for some suitable regular element $x$. Each regular element belongs to one and only one Cartan subalgebra. The dimension of all the Cartan subalgebras of $8$ are the same and are equal to the rank of $8$. The image of a Cartan subalgebra under a surjective homomorphism of Lie algebras is a Cartan subalgebra. If $k$ is algebraically closed, then all Cartan subalgebras of $8$ are conjugate; more precisely, they can be transformed into another by operators of the algebraic group $\Omega$ of automorphisms of $8$ whose Lie algebra is the commutator subalgebra of $g$. If $8$ is solvable, then the above assertion holds without the hypothesis that $k$ be algebraically closed.
Let $k$ be either a connected linear algebraic group over an algebraically closed field $k$ of characteristic zero, or a connected Lie group, and let $8$ be its Lie algebra. Then a subalgebra $1$ of $8$ is a Cartan subalgebra if and only if it is the Lie algebra of a Cartan subgroup of $k$.
Let $8$ be a subalgebra of the Lie algebra $\mathfrak { d } ( V )$ of all endomorphisms of a finite-dimensional vector space $V$ over $k$, and let $8$ be the smallest algebraic Lie algebra in $\mathfrak { d } ( V )$ containing $8$ (cf. Lie algebra, algebraic). If $1$ is a Cartan subalgebra of $8$, then 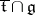 is a Cartan subalgebra of $8$, and if $1$ is a Cartan subalgebra of $8$ and $1$ is the smallest algebraic subalgebra of $\mathfrak { d } ( V )$ containing $1$, then $1$ is a Cartan subalgebra of $8$ and $t = \overline { t } \cap g$.
is a Cartan subalgebra of $8$, and if $1$ is a Cartan subalgebra of $8$ and $1$ is the smallest algebraic subalgebra of $\mathfrak { d } ( V )$ containing $1$, then $1$ is a Cartan subalgebra of $8$ and $t = \overline { t } \cap g$.
Let $k \subset K$ be a field extension. A subalgebra $1$ of $8$ is a Cartan subalgebra if and only if $t \otimes _ { k } K$ is a Cartan subalgebra of $g \otimes k ^ { K }$.
Cartan subalgebras play an especially important role when $8$ is a semi-simple Lie algebra (this was used by E. Cartan [1]). In this case, every Cartan subalgebra $1$ of $8$ is Abelian and consists of semi-simple elements (see Jordan decomposition), and the restriction of the Killing form to $1$ is non-singular.
References
| [1] | E. Cartan, "Sur la structure des groupes de transformations finis et continus" , Paris (1894) Zbl 25.0638.02 |
| [2] | N. Jacobson, "Lie algebras" , Interscience (1962) ((also: Dover, reprint, 1979)) MR0148716 MR0143793 Zbl 0121.27504 Zbl 0109.26201 |
| [3] | C. Chevalley, "Theory of Lie groups" , 1 , Princeton Univ. Press (1946) MR0082628 MR0015396 Zbl 0063.00842 |
| [4] | , Theórie des algèbres de Lie. Topologie des groupes de Lie , Sem. S. Lie , Ie année 1954–1955 , Ecole Norm. Sup. (1955) Zbl 0068.02102 |
Comments
An element $h \in \mathfrak { q }$ is called regular if the dimension of the Fitting null-component of the endomorphism $h$ of $8$ is minimal. "Almost-all" elements of $8$ are regular in the sense that the condition of being regular defines a Zariski-open subset. The result that the Fitting null-component of $h$ for $h$ regular is a Cartan subalgebra holds for finite-dimensional Lie algebras over any infinite field [a4], p. 59.
References
| [a1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002 |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004 |
| [a3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [a4] | N. Jacobson, "Lie algebras" , Dover, reprint (1979) ((also: Dover, reprint, 1979)) MR0559927 Zbl 0333.17009 Zbl 0215.38701 Zbl 0144.27103 Zbl 0121.27601 Zbl 0121.27504 Zbl 0109.26201 Zbl 0198.05404 Zbl 0064.27002 Zbl 0064.03503 Zbl 0046.03402 Zbl 0043.26803 Zbl 0039.02803 Zbl 0063.03015 Zbl 0025.30302 Zbl 0025.30301 Zbl 0022.19801 Zbl 0019.19402 Zbl 0018.10302 Zbl 0017.29203 Zbl 0016.20001 |
Maximilian Janisch/latexlist/Algebraic Groups/Cartan subalgebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximilian_Janisch/latexlist/Algebraic_Groups/Cartan_subalgebra&oldid=43990