Shafarevich conjecture
in inverse Galois theory
The absolute Galois group $G_{\textbf{Q}^{\text{ab}}}:=\text{Gal}(\overline{\textbf{Q}}/\textbf{Q}^{\text{ab}})$ of $\textbf{Q}^{\text{ab}}$ (cf. also Galois group) is a free profinite group of countable rank. Here, $\textbf{Q}^{\text{ab}}$ is the maximal Abelian extension of $\textbf{Q}$, or, equivalently (by the Kronecker–Weber theorem), the maximal cyclotomic extension of $\textbf{Q}$.
I.R. Shafarevich posed this assertion as an important problem during a 1964 series of talks at Oberwolfach on the solution to the class field tower problem (cf. Tower of fields; Class field theory). The conjecture would imply an affirmative answer to the inverse Galois problem over $\textbf{Q}^{\text{ab}}$, i.e. that every finite group is a Galois group over $\textbf{Q}^{\text{ab}}$ (cf. also Galois theory, inverse problem of). By the Iwasawa theorem [a7], p. 567, (see also [a1], Cor. 24.2), a profinite group $\Pi$ of countable rank is free (as a profinite group) if and only if every finite embedding problem for $\Pi$ has a proper solution. Thus, the Shafarevich conjecture is equivalent to the assertion that if $H$ is a quotient of a finite group $G$, then every $H$-Galois field extension of $\textbf{Q}^{\text{ab}}$ is dominated by a $G$-Galois field extension of $\textbf{Q}^{\text{ab}}$.
A weakening of this assertion is known: that the profinite group $G_{\textbf{Q}^{\text{ab}}}$ is projective, i.e. every finite embedding problem for $G_{\textbf{Q}^{\text{ab}}}$ has a weak solution (cf. also Projective group). Projectivity is equivalent to the condition of cohomological dimension $\leq 1$ [a12], Chap. 1; Props. 16, 45, and this holds for $G_{\textbf{Q}^{\text{ab}}}$ by [a12], Chap. 2; Prop. 9. On the other hand, the absolute Galois group $G_{\textbf{Q}}$ is not projective, since the surjection $G_{\textbf{Q}}\to\textbf{Z}/2\textbf{Z}$ corresponding to the extension $\textbf{Q}(i)/\textbf{Q}$ does not factor through $\textbf{Z}/4\textbf{Z}$. Thus, the analogue of the Shafarevich conjecture does not hold for $\textbf{Q}$.
Evidence for the conjecture.
Many finite groups, including "most" simple groups, have been realized as Galois groups over $\textbf{Q}^{\text{ab}}$ [a9], Chap. II, Sec. 10. These realizations provide evidence for the inverse Galois problem over $\textbf{Q}^{\text{ab}}$ and hence for the Shafarevich conjecture. Typically, these realizations have been achieved by constructing Galois branched covers of the projective line over $\textbf{Q}^{\text{ab}}$. Since $\textbf{Q}^{\text{ab}}$ is Hilbertian [a13], Cor. 1.28, such a realization implies that the covering group is a Galois group of a field extension of $\textbf{Q}^{\text{ab}}$. Most of these branched covers have been constructed by means of rigidity; cf. [a9] and [a13] for a discussion of this approach. (Some of these covers are actually defined over the $\textbf{Q}$-line, and their covering groups are thus Galois groups over $\textbf{Q}$.)
The rigidity approach also suggests a possible way of proving the Shafarevich conjecture. B.H. Matzat introduced the notion of GAR-realizability of a group, this being realizability as the Galois group of a branched cover with certain additional properties (cf. [a9], Chap. 4, Sec. 3.1). Many simple groups have been GAR-realized over $\textbf{Q}^{\text{ab}}$, and the Shafarevich conjecture would follow if it were shown that every finite simple group has a GAR-realization over $\textbf{Q}^{\text{ab}}$. See [a9], Chap. 4; Sec. 3, 4.
The solvable case of the Shafarevich conjecture has been proven: K. Iwasawa [a7] showed that the maximal pro-solvable quotient of $G_{\textbf{Q}^{\text{ab}}}$ is a free pro-solvable group of countable rank. In particular, every finite solvable group is a Galois group over $\textbf{Q}^{\text{ab}}$, and every embedding problem for $G_{\textbf{Q}^{\text{ab}}}$ with finite solvable kernel has a proper solution. Iwasawa's result also holds for the maximal Abelian extension $K^{\text{ab}}$ of any global field $K$, and for the maximal cyclotomic extension $K^{\text{cycl}}$ of any global field $K$ [a7], Thm. 6, 7.
Generalizations.
The Shafarevich conjecture can be posed with $\textbf{Q}$ replaced by any global field $K$. In this generalized form, it asserts that the absolute Galois group of $K^{\text{cycl}}$ is free of countable rank (as a profinite group). This conjecture remains open (as of 2001) in the number field case, but has been proven by D. Harbater [a6], Cor. 4.2, and F. Pop [a10] in the case that $K$ is the function field of a curve over a finite field $k$. (See also [a5], Cor. 4.7, and [a9], Sec. V.2.4.) Since $k^{\text{cycl}}=\textbf{F}_p$ if $k$ is a finite field of characteristic $p$, this assertion is equivalent to stating that the absolute Galois group of $K$ is free of countable rank if $K$ is the function field of a curve over $\textbf{F}_p$. This result is shown by using patching methods involving formal schemes or rigid analytic spaces, in order to show that all finite embedding problems for $G_K$ have a proper solution — i.e. that every connected $H$-Galois branched cover of the curve is dominated by a connected $G$-Galois branched cover, if $H$ is a quotient of the finite group $G$. By Iwasawa's theorem [a7], p. 567, the result follows. The proof also shows that if $C$ is a curve over an arbitrary algebraically closed field of cardinality $\kappa$, and if $K$ is the function field of $C$, then every finite embedding problem for $G_K$ has exactly $\kappa$ proper solutions. By the Mel'nikov–Chatzidakis theorem [a8], Lemma 2.1, it follows that $G_K$ is free profinite of rank $\kappa$, generalizing the geometric case of the Shafarevich conjecture (see [a6], Thm. 4.4, [a10], Cor. to Thm. A).
As another proposed generalization of the Shafarevich conjecture (which would subsume the above case of global fields), M. Fried and H. Völklein conjectured [a2], p. 470, that if $K$ is a countable Hilbertian field whose absolute Galois group $G_K$ is projective, then $G_K$ is free of countable rank. They proved a special case of this [a2], Thm. A, viz. that $G_K$ is free of countable rank if $K$ is a countable Hilbertian pseudo algebraically closed field (a PAC field) of characteristic $0$. For example, this applies to the field $K=\textbf{Q}^{\text{tr}}(\sqrt{-1})$, where $\textbf{Q}^{\text{tr}}$ is the field of totally real algebraic numbers, by results of R. Weissauer and Pop; see [a13], p. 151, [a9], p. 286. Later, Pop [a11], Thm. 1, removed the characteristic $0$ hypothesis from the above result. This solves a problem in [a1], Problem 24.41. (See also [a4].) Since $\textbf{Q}^{\text{ab}}$ is not PAC (as proven by G. Frey [a1], Cor.10.15), this result does not prove the Shafarevich conjecture itself. But it does imply that $G_{\textbf{Q}}$ has a free normal subgroup of countable rank for which the quotient is of the form $\prod^{\infty}_{n=2}S_n$ [a2] (instead of the form $\widehat{\textbf{Z}}^*=\text{Gal}(\textbf{Q}^{\text{ab}}$ as in the Shafarevich conjecture). The above Fried–Völklein conjecture holds if $K$ is Galois over $k(x)$, for $k$ an algebraically closed field ([a8], Prop. 4.4, using the geometric case of the Shafarevich conjecture [a6], [a10]). More generally, it holds if $K$ is large in the sense of Pop [a11], Thm. 2.1; cf. also [a9], Sec. V.4. A solvable case of the conjecture holds, extending Iwasawa's result: For $K$ Hilbertian with $G_K$ projective, every embedding problem for $G_K$ with finite solvable kernel has a proper solution [a13], Cor. 8.25.
References
| [a1] | M. Fried, M. Jarden, "Field arithmetic" , Springer (1986) |
| [a2] | M. Fried, H. Völklein, "The embedding problem over a Hilbertian PAC field" Ann. of Math. , 135 (1992) pp. 469–481 |
| [a3] | "Recent developments in the inverse Galois problem" M. Fried (ed.) , Contemp. Math. , 186 , Amer. Math. Soc. (1995) |
| [a4] | D. Haran, M. Jarden, "Regular split embedding problems over complete valued fields" Forum Math. , 10 (1998) pp. 329–351 |
| [a5] | D. Haran, H. Völklein, "Galois groups over complete valued fields" Israel J. Math. , 93 (1996) pp. 9–27 |
| [a6] | D. Harbater, "Fundamental groups and embedding problems in characteristic 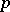 " M. Fried (ed.) , Recent Developments in the Inverse Galois Problem , Contemp. Math. , 186 , Amer. Math. Soc. (1995) pp. 353–370 " M. Fried (ed.) , Recent Developments in the Inverse Galois Problem , Contemp. Math. , 186 , Amer. Math. Soc. (1995) pp. 353–370 |
| [a7] | K. Iwasawa, "On solvable extensions of algebraic number fields" Ann. of Math. , 58 (1953) pp. 548–572 |
| [a8] | M. Jarden, "On free profinite groups of uncountable rank" M. Fried (ed.) , Recent Developments in the Inverse Galois Problem , Contemp. Math. , 186 , Amer. Math. Soc. (1995) pp. 371–383 |
| [a9] | G. Malle, B.H. Matzat, "Inverse Galois theory" , Springer (1999) |
| [a10] | F. Pop, "Étale Galois covers over smooth affine curves" Invent. Math. , 120 (1995) pp. 555–578 |
| [a11] | F. Pop, "Embedding problems over large fields" Ann. of Math. , 144 (1996) pp. 1–34 |
| [a12] | J.-P. Serre, "Cohomologie Galoisienne" , Lecture Notes in Mathematics , 5 , Springer (1964) |
| [a13] | H. Völklein, "Groups as Galois groups" , Studies in Adv. Math. , 53 , Cambridge Univ. Press (1996) |
Shafarevich conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shafarevich_conjecture&oldid=51550