Non-classical theory of models

non-classical model theory

A theory of models (cf. Model theory) that differs from the classical theory in the sense that either the relevant formal language is not the first-order language 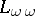, or the logic on which it is based is not the classical (two-valued) logic. In what follows, unless otherwise stated, the logic is assumed to be two-valued.

In the theory of models of a language 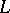the most important problems are the following.

a) The axiomatizability of the set of identically true formulas. If there is an effective enumeration of the formulas of the language by natural numbers, the problem becomes more precise: Is the set of numbers of the identically true formulas recursively enumerable?

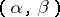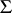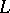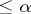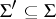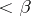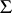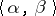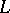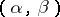b) A language is called -compact if for any set of propositions of of cardinality , realizability of every subset of cardinality implies realizability of . The compactness problem consists in describing the pairs of cardinal numbers for which is -compact.

c) If the formulas of 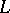form a set (rather than a proper class), then there is a cardinal number 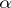such that every set of propositions of 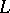that has a model of cardinality 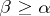also has models of arbitrarily large cardinalities. The least such cardinal number is called the Hanf number of 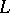. For 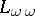this is the countable cardinal 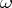. The problem consists in computing the Hanf number of 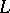and in establishing conditions for the existence of models of small cardinality.

Below the best studied non-classical languages are listed and for each of them solutions of the problems a)–c) are described.

1) The language 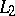of second-order logic. It is obtained from 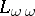by adding variables for predicates as well as quantifiers over such predicate-variables. A proposition 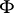of the language 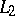is said to be true in a system 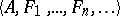(where 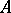is a model of signature and the 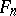, , 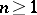are sets of -ary predicates on 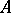) if is true in 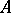for the restriction of the quantifiers to the -ary predicates in the sets 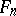. 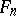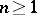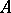If here , , are the sets of all -ary predicates on , then 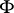is said to be true in the model 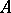. There is a proposition of the language 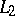that characterizes the arithmetic of natural numbers up to an isomorphism. From the Gödel incompleteness theorem for arithmetic it follows that the set of propositions of 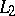that are true in all models is not axiomatizable. However, there is a natural generalization 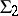of the axioms of first-order predicate calculus for which Henkin's completeness theorem holds: From 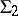those and only those propositions of 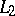are deducible that are true in all systems 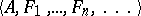satisfying the axioms of 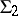. 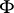In this case there is an analogue of the Löwenheim–Skolem theorem for : If a proposition of 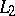is true together with the axioms of 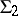in the same system, then 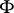and 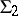are true in a system 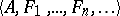, where 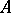and the 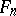, , 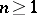are at most countable. Some questions in the theory of models of the language 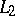are connected with problems of set theory and are unsolvable in the Zermelo–Fraenkel axiomatic set theory.

2) The language 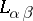(where 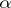and 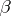are cardinal numbers). The formulas of this language are constructed from the formulas of the first-order language by means of conjunctions and disjunctions of sets of formulas of cardinality 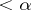and by negation and quantification over strings of variables of length 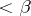. The truth of a formula in a model is defined, as in the first-order language, by induction on the structure of the formula. A cardinal number 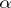is said to be compact if for any cardinal number 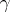the language 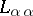is 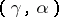-compact. Among the languages 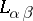, the best studied after 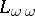is 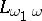. Every countable model of countable signature can be characterized by a proposition of the language up to an isomorphism. 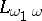The language is 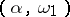-compact for any 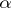. 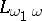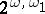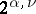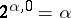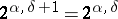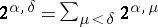The Hanf number of is , where is defined by induction over the ordinal numbers : , and when 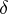is a limit ordinal.

3) The language with the quantifier "there exist at least wa many" . The language 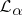is obtained from 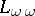by adding a new quantifier 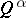. The truth of a formula is determined by induction on its length. Here a formula 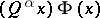is true in a model 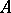if the cardinality of the set 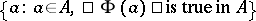is at leas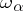t . Let 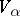denote the set of formulas of 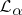that are true in all models of cardinality 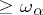. The set 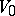is not axiomatizable, but 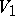is. The language 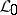is not 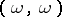-compact. However, a certain compactness holds in the languages 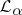. Let the symbol 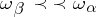indicate that 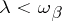and 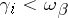(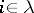) imply that 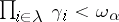. 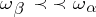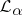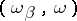If , then is -compact. The Hanf number of 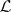is .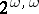

In the models considered so far any proposition of a language 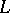of signature 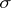was either true or false. Alternatively, one can consider models of signature 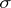in which -ary predicates are regarded not as subsets of 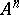but as mappings from 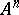into a set 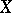. If on 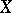operations corresponding to the logical connectives of the language 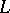and quantifiers (understood as infinitary operations) are defined, then one can define the truth value 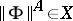of any proposition 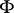of the language 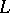in the model 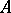. Thus one obtains a model theory with 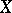as set of truth values. The theory is most fruitful in case 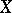is a compact Hausdorff space or a complete Boolean algebra. In these cases many methods of the classical theory of models work. When 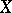is a complete Boolean algebra, then conjunction, disjunction and negation are defined as intersection, union and complementation, respectively. The value 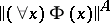is defined as the intersection of all elements of the form 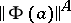, 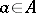. Boolean-valued models have found wide-spread application in proofs of the compatibility of various propositions of set theory with the basic axioms of axiomatic set theory.

References

[1]	A. Church, "Introduction to mathematical logic" , 1 , Princeton Univ. Press (1956)
[2]	C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973)

Comments

Additional references on infinitary logic are [a1], [a2].

References

[a1]	H.J. Keisler, "Model theory for infinitary logic" , North-Holland (1971)
[a2]	M.A. Dickmann, "Large infinitary languages" , North-Holland (1975)