Semi-cubic parabola

2020 Mathematics Subject Classification: Primary: 53A04 [MSN][ZBL]

A third-order algebraic curve in the plane whose equation in Cartesian coordinates is

$$y=ax^{3/2}.$$

The origin is a cusp (see Fig.). The length of the arc from the origin equals

$$l=\frac{1}{27a^2}[(4+9a^2x)^{2/3}-8];$$

and the curvature equals

$$k=\frac{6a}{\sqrt x(4+9a^2x)^{3/2}}.$$

A semi-cubic parabola is sometimes called a Neil parabola, after W. Neil who found its arc length in 1657.

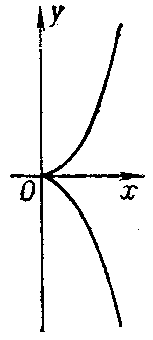
Figure: s084040a

References

[1]	A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)
[2]	A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian)

References

[a1]	J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972)
[a2]	F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971)