Convex subgroup of a partially ordered group
A subgroup 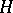 of a
of a 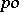 -group
-group 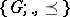 such that for all
such that for all 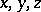 ,
,
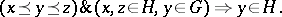 |
Many properties of po-groups can be described in terms of convex subgroups. If 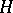 is convex subgroup of a po-group
is convex subgroup of a po-group 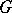 , then the set
, then the set 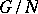 of right cosets of
of right cosets of 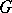 by
by 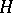 is partially ordered with the induced order:
is partially ordered with the induced order: 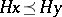 if there exists an element
if there exists an element 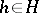 such that
such that 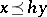 .
.
The set 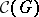 of all convex subgroups of a totally ordered group
of all convex subgroups of a totally ordered group 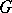 (cf.
(cf.  -group) is well investigated. It is a complete chain, i.e., it is closed with respect to join and intersection. The system
-group) is well investigated. It is a complete chain, i.e., it is closed with respect to join and intersection. The system 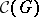 is infra-invariant, i.e.,
is infra-invariant, i.e., 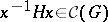 for all
for all 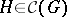 ,
, 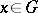 . If
. If 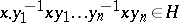 for
for 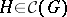 ,
, 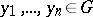 , then
, then 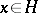 . For an element
. For an element 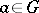 there exist a maximal subgroup
there exist a maximal subgroup 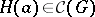 with the property
with the property 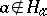 , and a minimal subgroup
, and a minimal subgroup 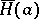 with the property
with the property 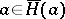 . The subgroup
. The subgroup 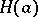 is normal in
is normal in 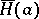 (cf. Normal subgroup) and the quotient group
(cf. Normal subgroup) and the quotient group 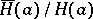 is order isomorphic to some subgroup of the additive group
is order isomorphic to some subgroup of the additive group 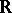 of real numbers. If
of real numbers. If 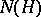 is the normalizer of the subgroup
is the normalizer of the subgroup 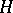 (cf. also Normalizer of a subset), then
(cf. also Normalizer of a subset), then 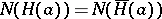 and
and  for every element
for every element 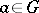 ,
, 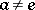 . Here,
. Here, 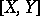 denotes the commutator subgroup of
denotes the commutator subgroup of 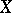 and
and 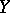 . If, in a group
. If, in a group 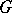 , one can find a system
, one can find a system 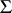 with the properties listed above, then it is possible to turn
with the properties listed above, then it is possible to turn 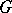 into an
into an  -group such that
-group such that 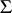 is the system of convex subgroups for
is the system of convex subgroups for 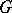 .
.
If 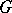 is a locally nilpotent o-group, then the system
is a locally nilpotent o-group, then the system 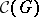 is a central system of subgroups.
is a central system of subgroups.
The set 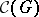 of all convex
of all convex 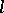 -subgroups (i.e., subgroups of
-subgroups (i.e., subgroups of 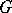 that are sublattices of the lattice
that are sublattices of the lattice 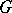 ) is very important for the description of the structure of an
) is very important for the description of the structure of an 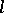 -group
-group 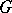 . It is a complete sublattice of the subgroup lattice of
. It is a complete sublattice of the subgroup lattice of 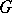 . If
. If 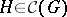 , then
, then 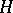 is isolated, i.e.,
is isolated, i.e., 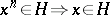 . A subset
. A subset 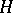 of an
of an 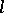 -group
-group 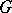 is the kernel of an
is the kernel of an 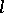 -homomorphism of
-homomorphism of 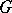 if and only if
if and only if 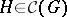 ; in that case it is a normal subgroup of
; in that case it is a normal subgroup of 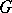 .
.
Also very important for describing the structure of an 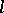 -group
-group 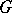 are the prime
are the prime 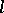 -subgroups, i.e., the convex
-subgroups, i.e., the convex 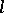 -subgroups
-subgroups 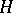 of
of 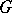 such that the partially ordered set
such that the partially ordered set 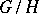 of right cosets is a chain. An
of right cosets is a chain. An 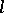 -subgroup
-subgroup 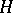 is prime if and only if it is convex and
is prime if and only if it is convex and 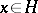 when
when 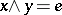 for elements
for elements 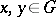 ,
, 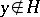 . If
. If 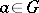 ,
, 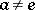 ,
, 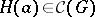 and
and 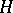 is maximal with respect to the property
is maximal with respect to the property 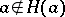 , then
, then 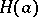 is prime. If
is prime. If 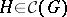 , then
, then 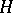 is the intersection of a suitable set of prime subgroups. If
is the intersection of a suitable set of prime subgroups. If 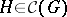 , then there exists a natural
, then there exists a natural 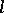 -homomorphism from
-homomorphism from 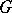 onto a transitive
onto a transitive 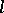 -subgroup of the
-subgroup of the 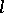 -group
-group 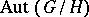 , where
, where 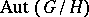 is the group of order automorphisms of the totally ordered set
is the group of order automorphisms of the totally ordered set 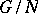 of right cosets.
of right cosets.
If 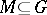 in an
in an 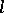 -group
-group 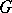 , then the set
, then the set
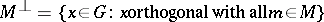 |
is called a polar and  .
.
This article complements and updates the article Convex subgroup (in Volume 2).
References
| [a1] | L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963) |
| [a2] | A. Bigard, K. Keimel, S. Wolfenstein, "Groupes et anneaux rétiqulés" , Springer (1977) |
| [a3] | "Lattice-ordered groups: advances and techniques" A.M.W. Glass (ed.) W.Ch. Holland (ed.) , Kluwer Acad. Publ. (1989) |
| [a4] | V.M. Kopytov, N.Ya. Medvedev, "The theory of lattice-ordered groups" , Kluwer Acad. Publ. (1994) (In Russian) |
Convex subgroup of a partially ordered group. V.M. Kopytov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_subgroup_of_a_partially_ordered_group&oldid=15705