Convex sequence
From Encyclopedia of Mathematics
A sequence of real numbers 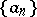 ,
, 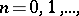 satisfying the condition
satisfying the condition
 | (*) |
Putting
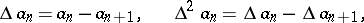 |
condition (*) may be written as
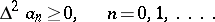 |
The geometrical meaning of condition (*) is that the broken line in the (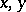 )-plane with corners at the points
)-plane with corners at the points  ,
, 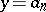 is convex. If the sequence
is convex. If the sequence 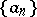 is both convex and bounded, then:
is both convex and bounded, then:
1) it does not increase and thus converges to a finite limit;
2) 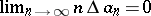 ;
;
3) 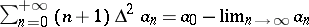 .
.
If 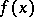 is a convex function (of a real variable) for
is a convex function (of a real variable) for 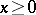 , the sequence
, the sequence 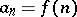 ,
, 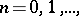 is convex.
is convex.
How to Cite This Entry:
Convex sequence. L.D. Kudryavtsev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_sequence&oldid=16907
Convex sequence. L.D. Kudryavtsev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_sequence&oldid=16907
This text originally appeared in Encyclopedia of Mathematics - ISBN 1402006098