Convergence, discrete
Convergence of functions and operators on lattices in corresponding spaces. Let 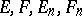
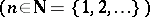 be Banach spaces, and let
be Banach spaces, and let 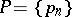 and
and 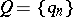 be systems of linear operators (connecting mappings)
be systems of linear operators (connecting mappings) 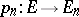 ,
, 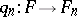 , with the property
, with the property
 |
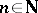 , for all
, for all 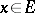 ,
, 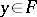 ,
,
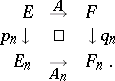 |
A sequence 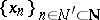 with
with 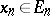 :
:
a) converges discretely (or 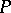 -converges) to
-converges) to 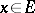 if
if 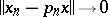
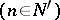 ;
;
b) is discretely compact (or 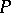 -compact) if for every infinite set
-compact) if for every infinite set 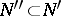 there is an infinite set
there is an infinite set 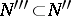 such that the subsequence
such that the subsequence 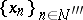 converges discretely.
converges discretely.
A sequence 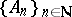 of operators
of operators 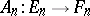 :
:
a) converges discretely (or 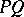 -converges) to an operator
-converges) to an operator 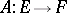 if for any
if for any 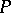 -convergent sequence
-convergent sequence 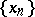 the relation
the relation
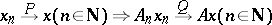 | (1) |
holds;
b) converges compactly to 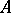 if, in addition to (1), the following condition is fulfilled:
if, in addition to (1), the following condition is fulfilled: 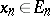 ,
, 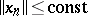 (
(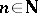 )
) 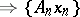 is
is  -compact;
-compact;
c) converges regularly (or properly) to 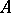 if, in addition to (1), the following condition is fulfilled:
if, in addition to (1), the following condition is fulfilled: 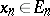 ,
, 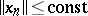 ,
, 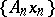 is
is  -compact
-compact 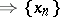 is
is 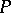 -compact;
-compact;
d) converges stably to 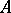 if, in addition to (1), the following condition is fulfilled: There exists an
if, in addition to (1), the following condition is fulfilled: There exists an 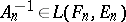 such that
such that 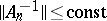
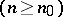 .
.
Let 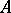 and
and 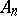 be bounded linear operators. Then
be bounded linear operators. Then 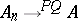 if and only if
if and only if 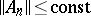
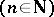 and if
and if 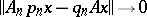 for every
for every  from a certain dense subset in
from a certain dense subset in 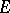 .
.
For bounded linear operators 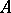 and
and 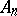 , the following conditions are equivalent:
, the following conditions are equivalent:
1) 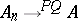 stably,
stably, 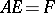 ;
;
2) 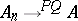 regularly,
regularly, 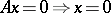 , and the operators
, and the operators 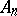
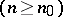 are Fredholm operators with index zero;
are Fredholm operators with index zero;
3) 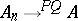 stably and regularly.
stably and regularly.
If one of these conditions is fulfilled, then 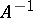 and
and 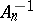 (for sufficiently large
(for sufficiently large  ) exist, and
) exist, and  stably and regularly. If the conditions 1), 2) and 3) are fulfilled, they can be interpreted as a convergence theorem for the equations
stably and regularly. If the conditions 1), 2) and 3) are fulfilled, they can be interpreted as a convergence theorem for the equations 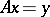 and
and 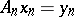 : If 1), 2) or 3) are fulfilled, then
: If 1), 2) or 3) are fulfilled, then 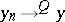 implies that
implies that
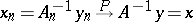 |
with rate
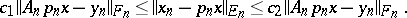 |
In proving the convergence of approximate methods, 1) and 2) are used most frequently. Appropriate spaces of functions are chosen for 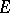 and
and 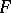 , while operators that transfer the functions to their values on a lattice are chosen for
, while operators that transfer the functions to their values on a lattice are chosen for 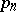 and
and 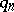 .
.
References
| [1a] | F. Stummel, "Diskrete Konvergenz linearer Operatoren I" Math. Ann. , 190 (1970) pp. 45–92 |
| [1b] | F. Stummel, "Diskrete Konvergenz linearer Operatoren II" Math. Z. , 120 (1971) pp. 231–264 |
| [2] | G.M. Vainikko, "Regular convergence of operators and approximate solution of equations" J. Soviet Math. , 15 (1981) pp. 675–705 Itogi Nauk. i Tekhn. Mat. Anal. , 16 (1979) pp. 5–53 |
| [3] | G.M. Vainikko, "Funktionalanalysis der Diskretisierungsmethoden" , Teubner (1976) (Translated from Russian) |
Convergence, discrete. G.M. Vainikko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convergence,_discrete&oldid=13267