Control function
control
A function 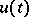 occurring in a differential equation
occurring in a differential equation
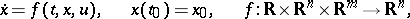 | (1) |
and the values of which at each moment of time may be chosen arbitrarily.
Usually the domain of variation of 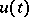 , for each
, for each  , is subject to a restriction
, is subject to a restriction
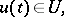 | (2) |
where  is a given closed set in
is a given closed set in 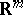 . A control is called admissible if for each
. A control is called admissible if for each  it satisfies the constraint (2). Different admissible controls
it satisfies the constraint (2). Different admissible controls 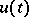 define corresponding trajectories
define corresponding trajectories 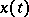 , starting from the initial point
, starting from the initial point 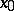 .
.
If one is given a functional
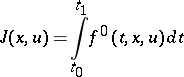 | (3) |
and a boundary condition at the right-hand end of the trajectory at 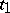 :
:
 | (4) |
where 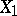 is a certain set in
is a certain set in 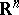 (in a special case, a single point), then one may raise the question of determining an optimal control
(in a special case, a single point), then one may raise the question of determining an optimal control 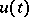 , giving an optimal value for the functional in the problem (1)–(4). Questions connected with the definition of optimal control functions have been considered in the theory of optimal control and variational calculus (cf. [1], [2]).
, giving an optimal value for the functional in the problem (1)–(4). Questions connected with the definition of optimal control functions have been considered in the theory of optimal control and variational calculus (cf. [1], [2]).
In distinction to the variables 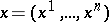 , called phase variables (or phase coordinates), the control
, called phase variables (or phase coordinates), the control 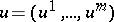 occurs in equation (1) without derivatives. Therefore (1) has a meaning not only for continuous, but also for piecewise-continuous (and even measurable) controls
occurs in equation (1) without derivatives. Therefore (1) has a meaning not only for continuous, but also for piecewise-continuous (and even measurable) controls 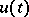 . Moreover, for each admissible piecewise-continuous control
. Moreover, for each admissible piecewise-continuous control 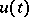 equation (1) defines a continuous piecewise-smooth trajectory
equation (1) defines a continuous piecewise-smooth trajectory 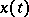 .
.
In the majority of problems an optimal control exists in the class of piecewise-continuous functions. However, one meets with problems in which the optimal control is not piecewise continuous, but belongs to the class of Lebesgue-measurable functions. In these cases the optimal control has an infinite number of points of discontinuity, approaching a certain point, for example, an entry point for a singular surface of order 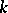 ,
, 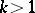 (cf. Optimal singular regime).
(cf. Optimal singular regime).
Necessary conditions, formulated in the theory of optimal control in the form of Pontryagin's maximum principle, have been proved in the general case in which the optimal control function being studied is assumed measurable (in particular, it may be piecewise continuous or continuous).
According to the maximum principle, for 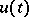 to be an optimal control (in the case of minimization of the functional (3)) it is necessary that for each
to be an optimal control (in the case of minimization of the functional (3)) it is necessary that for each 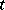 the control gives a maximum of the Hamiltonian
the control gives a maximum of the Hamiltonian
 |
on 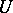 , where
, where 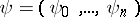 is a conjugate vector function, defined by the conjugate system
is a conjugate vector function, defined by the conjugate system
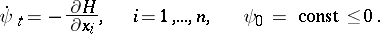 |
An analogous maximum principle in the calculus of variations allows one to define "free" functions under constraints given by the Euler equations and the Weierstrass necessary condition.
For the existence of an optimal Lebesgue-measurable control giving a minimum of the functional (3) it is sufficient that for each 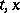 the set of values of the vector on the right-hand side,
the set of values of the vector on the right-hand side, 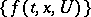 , obtained as the control
, obtained as the control  ranges over all admissible values of the domain
ranges over all admissible values of the domain 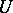 , is convex in
, is convex in 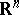 , and that the greatest lower bound
, and that the greatest lower bound 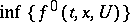 of the set of values assumed by the integrand is convex from below as a function in
of the set of values assumed by the integrand is convex from below as a function in  . If this condition is not fulfilled, there may be cases where the minimizing sequence of controls
. If this condition is not fulfilled, there may be cases where the minimizing sequence of controls 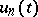 no longer converges, even in the class of measurable functions. In these cases one says that one has a sliding (or relaxed) optimal regime (control). A sliding optimal control may be given in a strict sense as a singular optimal control in a related problem closely connected with the initial one (cf. Optimal sliding regime).
no longer converges, even in the class of measurable functions. In these cases one says that one has a sliding (or relaxed) optimal regime (control). A sliding optimal control may be given in a strict sense as a singular optimal control in a related problem closely connected with the initial one (cf. Optimal sliding regime).
Using the necessary as well as the sufficient conditions for optimality established in the theory of optimal control and the calculus of variations one may define optimal control functions and the corresponding optimal phase trajectories in the problems being considered. There are different numerical methods for constructing optimal controls (cf. Variational calculus, numerical methods of).
In more general cases the control function may depend on several arguments. In that case one speaks of a control function with distributed parameters.
References
| [1] | L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian) |
| [2] | G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947) |
| [3] | I.B. Vapnyarskii, "An existence theorem for optimal control in the Bolza problem, some of its applications and the necessary conditions" USSR Comp. Math. Math. Phys. , 7 (1963) pp. 22–54 Zh. Vychisl. Mat. i. Mat. Fis. , 7 : 2 (1967) pp. 259–283 |
| [4] | A.G. Butkovskii, "Theory of optimal control of systems with distributed parameters" , Moscow (1965) (In Russian) |
Comments
Formula (1) may be interpreted in two ways. Either 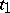 is fixed and the state
is fixed and the state  must belong to
must belong to 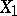 at
at 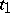 , or
, or  is implicitly determined by the problem, i.e. there must be a
is implicitly determined by the problem, i.e. there must be a 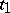 such that
such that 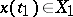 .
.
In Western literature phase variables or phase coordinates are usually referred to as state variables or state coordinates. The maximum principle of Pontryagin yields necessary conditions for the optimal control function as a function of time; 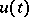 . This is sometimes called open-loop control, in contrast to closed-loop control where the optimal control is considered to be a function of the state as well;
. This is sometimes called open-loop control, in contrast to closed-loop control where the optimal control is considered to be a function of the state as well; 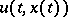 .
.
Standard texts are [a1], [a2].
References
| [a1] | A.E. Bryson, Y.-C. Ho, "Applied optimal control" , Hemisphere (1975) |
| [a2] | W.H. Fleming, R.W. Rishel, "Deterministic and stochastic optimal control" , Springer (1975) |
Control function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Control_function&oldid=16659