Contragredient automorphism

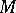to an automorphism of a right module over a ring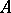

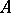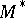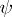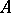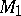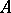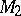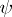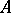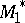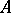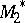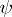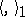The automorphism of the left -module (* denotes taking the dual or adjoint module) that is adjoint to the inverse automorphism to . More generally, if is an automorphism between a right -module and a right -module , then the contragredient isomorphism to is the isomorphism of the left -module onto the left -module that is adjoint to the inverse of the isomorphism . Let and 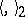be the canonical bilinear forms on 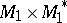and 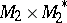. Then 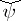is defined by the following identity with respect to , :

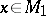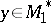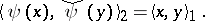If 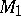and have finite bases, then is the isomorphism contragredient to .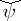

Let 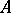be a ring with an identity, let 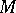be a right 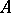-module with a finite basis, let 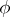be an automorphism of 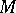, and let 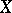be the matrix of 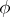in a fixed basis (this matrix is invertible). Then in the dual basis, the matrix of the contragredient automorphism 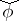has the form

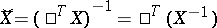(here denotes the transpose). The matrix 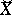is called the matrix contragredient to the invertible matrix .

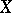References

[1]	N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French)

Comments

Instead of adjoint module and adjoint automorphism one also uses dual module and dual automorphism (cf. Adjoint module; Automorphism).