Contracting-mapping principle
contractive-mapping principle, contraction-mapping principle
A theorem asserting the existence and uniqueness of a fixed point of a mapping 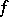 of a complete metric space
of a complete metric space  (or a closed subset of such a space) into itself, if for any
(or a closed subset of such a space) into itself, if for any  the inequality
the inequality
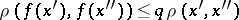 | (1) |
holds, for some fixed  ,
, 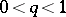 . This principle is widely used in the proof of the existence and uniqueness of solutions not only of equations of the form
. This principle is widely used in the proof of the existence and uniqueness of solutions not only of equations of the form 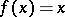 , but also of equations
, but also of equations 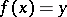 , by changing the equation to the equivalent:
, by changing the equation to the equivalent:  , where
, where 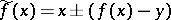 .
.
The scheme of application of the principle is usually as follows: Starting from the properties of 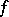 first find a closed set
first find a closed set 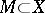 , usually a closed ball, such that
, usually a closed ball, such that 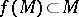 , and then prove that on this set
, and then prove that on this set  is a contractive mapping. After this, starting from an arbitrary element
is a contractive mapping. After this, starting from an arbitrary element 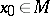 , construct the sequence
, construct the sequence  ,
, 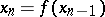 ,
, 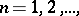 belonging to
belonging to 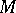 , which converges to some element
, which converges to some element  . This will be the unique solution of the equation
. This will be the unique solution of the equation  , and
, and 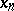 will be a sequence of approximate solutions.
will be a sequence of approximate solutions.
In general, condition (1) cannot be changed to
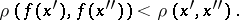 | (2) |
However, if this condition is satisfied on a compact set 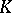 that is mapped into itself by
that is mapped into itself by  , then it guarantees the existence of a unique fixed point
, then it guarantees the existence of a unique fixed point 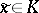 for
for  .
.
The following generalization of the contractive-mapping principle holds. Again, let  map a complete metric space
map a complete metric space 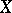 into itself and let
into itself and let
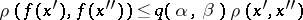 |
for 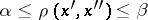 , where
, where 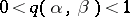 for
for  . Then
. Then 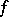 has a unique fixed point in
has a unique fixed point in  .
.
References
| [1] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [2] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [3] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) |
| [4] | V. Trenogin, "Functional analysis" , Moscow (1980) (In Russian) |
Comments
This principle is also known as the contraction principle or Banach's fixed-point theorem. It was proved by S. Banach in [a1]. The generalization discussed at the end of the article above goes by the name generalized contraction mapping in the sense of Krasnosel'skii [a5], [a6]. For this and other generalizations of the idea of a contractive mapping, cf. [a4], Chapt. 3.
References
| [a1] | S. Banach, "Sur les opérations dans les ensembles abstraits et leurs application aux équations intégrales" Fund. Math. , 3 (1922) pp. 7–33 |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1953) |
| [a3] | S. Willard, "General topology" , Addison-Wesley (1970) |
| [a4] | V.I. Istrăţescu, "Fixed point theory" , Reidel (1981) |
| [a5] | M.A. Krasnosel'skii, "Topological methods in the theory of nonlinear integral equations" , Macmillan (1964) (Translated from Russian) |
| [a6] | M.A. Krasnosel'skii, "Positive solutions of operator equations" , Noordhoff (1964) (Translated from Russian) |
Contracting-mapping principle. V.I. Sobolev (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contracting-mapping_principle&oldid=12147