Continuous series of representations
principal series of representations
The family of irreducible unitary representations of a locally compact group 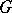 that occur in the decomposition of the regular representation of
that occur in the decomposition of the regular representation of 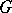 , but do not belong to the discrete series (of representations) of this group. If
, but do not belong to the discrete series (of representations) of this group. If 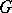 is a real semi-simple Lie group,
is a real semi-simple Lie group, 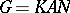 is its Iwasawa decomposition and
is its Iwasawa decomposition and 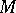 is the centralizer of
is the centralizer of 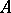 in
in 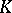 , then the non-degenerate continuous principal series of representations of
, then the non-degenerate continuous principal series of representations of 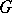 is the family of irreducible unitary representations of
is the family of irreducible unitary representations of 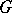 induced by the finite-dimensional irreducible unitary representations of the group
induced by the finite-dimensional irreducible unitary representations of the group 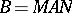 that are trivial on
that are trivial on 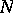 .
.
The complementary (or degenerate) continuous series of representations of such a group 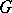 is the family of irreducible unitary representations of
is the family of irreducible unitary representations of 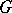 that occur in the complementary series (of representations) (respectively, the degenerate series of representations) of
that occur in the complementary series (of representations) (respectively, the degenerate series of representations) of 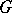 and are not isolated points of it (as subsets of the dual space of
and are not isolated points of it (as subsets of the dual space of 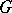 ). The analytic continuation of the non-degenerate continuous principal series of representations is the family of (generally speaking, non-unitary) representations of
). The analytic continuation of the non-degenerate continuous principal series of representations is the family of (generally speaking, non-unitary) representations of 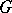 induced by all possible finite-dimensional irreducible representations of
induced by all possible finite-dimensional irreducible representations of 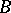 that are trivial on
that are trivial on 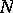 . This family plays a decisive role in the representation theory of real semi-simple Lie algebras and harmonic analysis on these groups; in particular, any completely irreducible representation of
. This family plays a decisive role in the representation theory of real semi-simple Lie algebras and harmonic analysis on these groups; in particular, any completely irreducible representation of 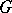 in a Hilbert space is infinitesimally equivalent to a subrepresentation of some quotient representation of one of the representations of the analytic continuation of the non-degenerate continuous principal series of representations. See also Infinite-dimensional representation of a Lie group.
in a Hilbert space is infinitesimally equivalent to a subrepresentation of some quotient representation of one of the representations of the analytic continuation of the non-degenerate continuous principal series of representations. See also Infinite-dimensional representation of a Lie group.
References
| [1] | I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian) |
| [2] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [3] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , 1–2 , Springer (1972) |
Comments
In the Western literature one customarily uses the terminology principal series instead of non-degenerate continuous principal series. Note that 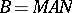 as above is a minimal parabolic subgroup. One even speaks of a (generalized) principal series representation in the following situation. Let
as above is a minimal parabolic subgroup. One even speaks of a (generalized) principal series representation in the following situation. Let 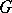 be a connected semi-simple matrix group and let
be a connected semi-simple matrix group and let 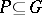 be a cuspidal (not necessarily minimal) parabolic subgroup. Fix a Langlands decomposition
be a cuspidal (not necessarily minimal) parabolic subgroup. Fix a Langlands decomposition 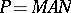 with
with 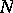 the unipotent radical and
the unipotent radical and 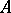 a vector group. Let
a vector group. Let 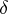 be a discrete series representation of
be a discrete series representation of 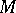 and
and  a (non-unitary) character of
a (non-unitary) character of 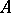 . The induced representation
. The induced representation
 |
is called a generalized principal series representation. When  is unitary, these are the representations occurring in Harish-Chandra's Plancherel formula for
is unitary, these are the representations occurring in Harish-Chandra's Plancherel formula for 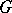 . The result mentioned at the end of the entry above usually is called the subquotient theorem: Any irreducible admissible representation of
. The result mentioned at the end of the entry above usually is called the subquotient theorem: Any irreducible admissible representation of 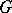 can be realized canonically as a subquotient of a generalized principal series representation.
can be realized canonically as a subquotient of a generalized principal series representation.
References
| [a1] | A.W. Knopp, "Representation of semisimple groups" , Princeton Univ. Press (1986) |
| [a2] | D.A. Vogan jr., "Representations of real reductive Lie groups" , Birkhäuser (1981) |
Continuous series of representations. A.I. Shtern (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_series_of_representations&oldid=12832