Continuous fraction
The same as continued fraction, i.e. an expression of the form
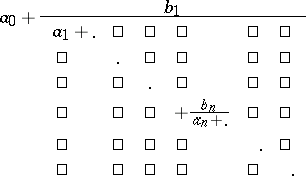 |
where
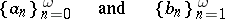 |
are finite or infinite sequences of complex numbers or functions. For continued fractions one uses the notation
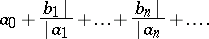 | (*) |
As a rule, it is assumed that the sequences  and
and  are such that for all
are such that for all  ,
,  ,
,
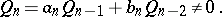 |
(The  are defined recursively, with
are defined recursively, with 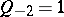 ,
, 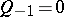 .)
.)
Comments
In translations the phrase continuous fraction occurs occasionally instead of continued fraction.
The notation (*) is due to A. Pringsheim, cf. [a1] for other notations.
The number or function obtained by evaluation of the truncation
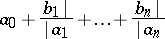 |
is called the  -th convergent of the continued fraction. It equals
-th convergent of the continued fraction. It equals 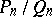 where
where  satisfy the recursion given above (with
satisfy the recursion given above (with  ) and starting values
) and starting values 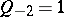 ,
, 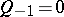 ;
; 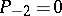 ,
,  . If the convergents
. If the convergents 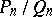 tend to a limit as
tend to a limit as 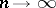 , one says that the continued fraction converges.
, one says that the continued fraction converges.
Continued fractions play an important role in number theory, in particular in Diophantine approximation, where  ,
, 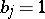 , in ergodic theory, again with
, in ergodic theory, again with 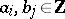 , and in numerical mathematics, where
, and in numerical mathematics, where 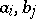 are rational functions. Famous examples of explicit continued fractions are those for hypergeometric functions such as
are rational functions. Famous examples of explicit continued fractions are those for hypergeometric functions such as
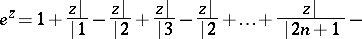 |
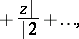 |
whose corresponding  's are orthogonal polynomials. In number theory the most famous is the golden ratio
's are orthogonal polynomials. In number theory the most famous is the golden ratio
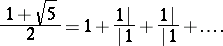 |
Good introductions to continued fractions in number theory are [a1], Chapt. X, [a2], in numerical mathematics [a3], and generally [a4].
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 |
| [a2] | A.Ya. [A.Ya. Khinchin] Khintchine, "Kettenbrüche" , Teubner (1956) (Translated from Russian) |
| [a3] | H.S. Wall, "Continued fractions" , v. Nostrand (1948) |
| [a4] | O. Perron, "Die Lehre von den Kettenbrüche" , 1–2 , Teubner (1954) |
Continuous fraction. O.A. Ivanova (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_fraction&oldid=13285