Continuous decomposition

of a topological space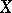

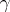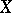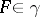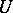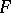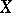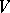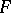A covering of by pairwise-disjoint non-empty sets satisfying the following condition: For any and any neighbourhood of in there is a neighbourhood of in 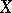contained in 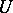that is the union of a certain collection of elements of 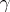. A decomposition is continuous if and only if the corresponding quotient mapping of 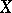onto the space of this decomposition is closed. A continuous mapping 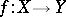of a space onto a space 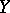is closed if and only if the decomposition 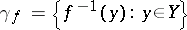of 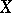is continuous.

Continuous decompositions occur frequently in the theory of compact spaces (cf. Compact space). Every continuous mapping of a compact space onto a Hausdorff space is closed. Therefore, every continuous mapping of a compact space 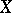onto a Hausdorff space 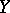gives rise to a continuous decomposition of 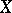by inverse images of points. For the same reason a decomposition of a Hausdorff compactum is continuous if (and only if) the space of this decomposition satisfies the Hausdorff separation axiom. The merit of a continuous decomposition of a space into closed sets is the preservation of normality and paracompactness. By way of contrast, the space of a continuous decomposition of a metric space into closed sets need not be metrizable. The simplest example of this situation is the space of the decomposition of the plane whose only non-trivial element is a fixed straight line.

Like decomposition in general, continuous decompositions are an important tool in the construction of new topological spaces from existing ones and also in the representation of more complicated topological spaces as the spaces of continuous decompositions of simpler or more standard spaces. Thus, every metrizable compactum is the space of a continuous decomposition of a Cantor set. Every connected, locally connected, metrizable compactum can be represented as the space of a continuous decomposition of an interval. Continuous decompositions occur naturally in certain specific constructions; for example, the projective plane, regarded as a topological space, is the space of the continuous decomposition of the ordinary sphere into pairs of diametrically-opposite points. Similarly, -dimensional projective space, from the topological point of view, is the space of the continuous decomposition of the -dimensional sphere, lying in 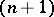-dimensional Euclidean space, into pairs of diametrically-opposite points. In this language, a Möbius strip can be described accurately as the space of a certain continuous decomposition of a rectangle, and other geometric objects can also be constructed in this way.

References

[1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)

Comments

The space of a decomposition 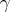of 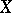has the set as underlying set, and 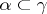is open if and only if 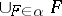is open in 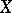. That is, it is the quotient space of 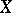defined by the equivalence relation 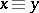if and only if and 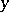both belong to the same element of .

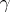A covering 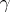satisfying the requirements of the article above is also called an upper semi-continuous decomposition. An equivalent definition is: For every closed set 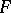the set 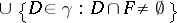is closed. A covering 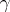is called a lower semi-continuous decomposition if 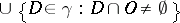is open for every open set 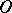. Equivalently: 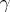is a lower semi-continuous decomposition if and only if the corresponding quotient mapping is open (cf. Open mapping).

Instead of "decomposition" the word "partitioning" is used.