Continuation method (to a parametrized family)

The inclusion of a given problem in a one-parameter family of problems, connecting the given problem with a problem that is known to be solvable , and the study of the dependence of solutions on the parameter . The method is extensively used in the theory of differential equations.

Suppose, e.g., that one has to prove the solvability in a Hölder class of the Dirichlet problem

(1)

in a suitable bounded -dimensional region for the linear elliptic second-order operator

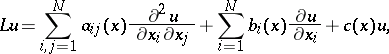One introduces the family of elliptic operators

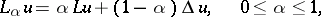and considers for it the Dirichlet problem

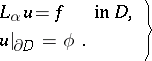(2)

Let 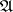be the set of all 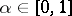for which (2) is uniquely solvable in for any 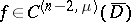and . The set 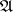is not empty, since for 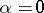(i.e. for the Laplace operator) (2) is uniquely solvable in , which follows from potential theory. The set 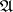is at the same time open and closed in 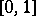, hence coincides with it. Thus, belongs to 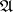and (1) is solvable.

The continuation method (in the case of analytic continuation) was proposed and developed in a number of papers by S.N. Bernstein [S.N. Bernshtein], cf. [1], [2]. Subsequently, this method gained wide application in various problems in the theory of linear and non-linear differential equations, where the idea of analytic continuation was supplemented by more general functional and topological principles (cf. [3]).

References

[1]	S.N. [S.N. Bernshtein] Bernstein, Math. Ann. , 59 (1904) pp. 20–76
[2]	S.N. Bernshtein, "Collected works" , 3 , Moscow (1960) (In Russian)
[3]	J. Leray, J. Schauder, Ann. Ecole Norm. Super. , 51 (1934) pp. 45–78

Comments

The idea of imbedding a given problem, e.g., a differential equation or an optimization problem, into a family of problems is quite old and has been rediscovered, independently, a number of times. It goes back at least to H. Poincaré [a1] and it was in fact a favorite technique of Poincaré.

In more recent times it arose one more time initially in the context of optimization problems and the calculation of economic equilibria starting with an algorithm of H. Scarf to calculate Brouwer fixed points [a2], in turn based on Sperner's lemma for labelling simplices during subdivision procedures. This is narrowly related to pivoting procedures [a3]. The Scarf algorithm and other related ones rapidly evolved into various algorithms for solving equations, for finding extrema and for tracing bifurcating solutions.

The families of problems in which the given problem is imbedded can be seen as a continuous deformation or homotopy of that problem, whence the names homotopy method, and homotopy continuation method for this class of methods. The phrases continuity method and predictor-corrector method also occur. A selection of recent literature on the topic is [a4]–[a9]. The survey paper [a4] has a very extensive bibliography. A substantial number of previously known algorithms for solving equations can be obtained as particular cases of the homotopy continuation method.

A rather different implementation of the general idea of imbedding a problem into suitable families of problems is provided by R. Bellmann's invariant imbedding method.

A more complete discussion and proof of the example of the Dirichlet problem above is given in [a10].

References

[a1]	H. Poincaré, "Sur les courbes définies par une équation différentielle I (1881)" , Oeuvres , I , Gauthier-Villars (1951)
[a2]	H. Scarf, "The approximation of fixed points of a continuous mapping" SIAM J. Appl. Math. , 15 (1967) pp. 1328–1343
[a3]	B. Curtis Eaves, "A view of complementary pivot theory (or solving equations with homotopies)" H.-O. Peitgen (ed.) H.-O. Walther (ed.) , Functional differential equations and approximation of fixed points , Lect. notes in math. , 730 , Springer (1979) pp. 89–111
[a4]	E. Allgower, K. Georg, "Simplicial and continuation methods for approximating fixed points and solutions to systems of equations" SIAM Review , 22 (1980) pp. 28–85
[a5]	B. Curtis Eaves, "A short course in solving equations with PL homotopies" , SIAM-AMS Proc. , 9 (1976) pp. 73–143
[a6]	S.L. Richter, R.A. DeCarlo, "Continuation methods: theory and applications" IEEE Trans. AC , 28 (1983) pp. 660–665
[a7]	H.-O. Peitgen (ed.) H.-O. Walther (ed.) , Functional differential equations and approximation of fixed points , Lect. notes in math. , 730 , Springer (1979)
[a8]	S. Karamurdian (ed.) , Fixed points. Algorithms and applications , Acad. Press (1977)
[a9]	H. Wacker (ed.) , Continuation methods , Acad. Press (1978)
[a10]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)