Contingency equation
From Encyclopedia of Mathematics
A relation
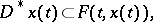 |
where 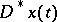 is the contingency of a vector function
is the contingency of a vector function 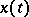 , i.e. the set of all partial limits of the ratio
, i.e. the set of all partial limits of the ratio
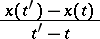 |
as  , while
, while 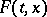 is a given non-empty set in
is a given non-empty set in 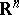 , depending on
, depending on 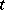 and
and  (cf. [1], [2]). If
(cf. [1], [2]). If 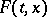 is a bounded closed convex set that is upper semi-continuous relative to the inclusion function of the point
is a bounded closed convex set that is upper semi-continuous relative to the inclusion function of the point 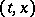 , the contingency equation is equivalent to the paratingency equation (defined analogously to the contingency equation, but using the ratio
, the contingency equation is equivalent to the paratingency equation (defined analogously to the contingency equation, but using the ratio
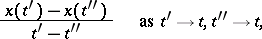 |
cf. [3]) and the differential inclusion
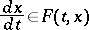 |
(cf. [4]). The properties of a contingency equation are similar to those of a differential inclusion.
References
| [1] | A. Marchaud, "Sur les champs de demi-cônes et les équations différentielle du premier ordre" Bull. Soc. Math. France , 62 (1934) pp. 1–38 |
| [2] | E.A. Barbashin, Yu.I. Alimov, "On the theory of relay differential equations" Izv. Vysshikh Uchebn. Zaved. Mat. : 1 (1962) pp. 3–13 (In Russian) |
| [3] | S.K. Zaremba, "Sur les équations au paratingent" Bull. Sci. Math. (2) , 60 : 5 (1936) pp. 139–160 |
| [4] | T. Waźewski, "Sur une condition équivalente à l'équation au contingent" Bull. Acad. Sci. Polon. Sci. Ser. Math. , 9 : 12 (1961) pp. 865–867 |
How to Cite This Entry:
Contingency equation. A.F. Filippov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contingency_equation&oldid=13474
Contingency equation. A.F. Filippov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contingency_equation&oldid=13474
This text originally appeared in Encyclopedia of Mathematics - ISBN 1402006098