Contextual grammar

A language-generating device based on the operation of adjoining contexts to strings, according to a selection procedure. Such grammars were introduced (in the external variant, with the contexts adjoined at the ends of the currently generated string) in [a2], with the explicit purpose of obtaining an intrinsic generative mechanism, without auxiliary symbols (as in Chomsky grammars) and making use of the string-context interplay which is fundamental in all linguistic theories. For modelling natural language-syntactical constructions, the internal contextual grammars, introduced in [a5], turned out to be more useful.

Let 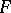be a family of languages. An internal contextual grammar with 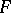-selection is a system

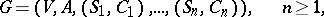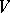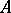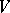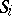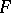where is an alphabet, is a finite language over , are languages (over ) in the family , and 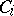are finite sets of contexts over , i.e., pairs 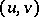, , 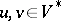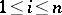. The elements of 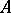are axioms, 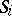are the selectors of the productions 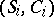, 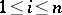. With respect to 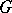, for 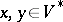one writes 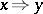if and only if 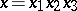, , 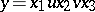with 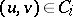, , 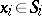for certain 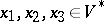, 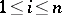. (The contexts in 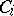can be adjoined to strings in the associated selector .)

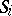Denoting by 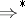the reflexive and transitive closure of 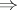, the language generated by 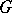can be defined by

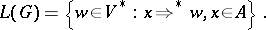Let 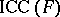be the family of languages generated by internal contextual grammars with 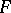-selection. Denote by 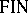, , 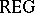, , 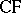, 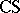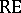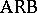the families of finite, regular, context-free, context-sensitive, recursively enumerable, and arbitrary languages, respectively. Some basic results for contextual grammars are as follows:

1) ;

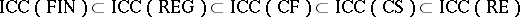2) , ;

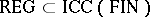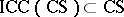3) 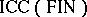contains non-semi-linear languages;

4) all families 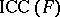, 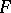as above, are anti-AFL (cf. Trio; Abstract family of languages);

5) every recursively enumerable language can be written in the form 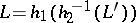, where 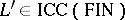, 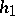is a weak coding and 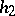is a morphism.

A lot of variants have been considered (left-most, prefix, parallel, blocked derivation, maximal or minimal use of selectors, one-sided contexts, deterministic grammars, etc.). Details can be found in [a1], [a3], [a4].

References

[a1]	A. Ehrenfeucht, Gh. Păun, G. Rozenberg, "Contextual grammars" G. Rozenberg (ed.) A. Salomaa (ed.) , Handbook of Formal Languages , Springer (1996)
[a2]	S. Marcus, "Contextual grammars" Rev. Roum. Math. Pures Appl. , 14 (1969) pp. 1525–1534
[a3]	Gh. Păun, "Contextual grammars" , Publ. House of the Romanian Acad., Bucharest (1982) (In Rumanian)
[a4]	Gh. Păun, "Marcus contextual grammars. After 25 years" Bull. EATCS , 52 (1994) pp. 263–273
[a5]	Gh. Păun, X.M. Nguyen, "On the inner contextual grammars" Rev. Roum. Math. Pures Appl. , 25 (1980) pp. 641–651