Bartlett test
From Encyclopedia of Mathematics
A statistical test in the Behrens–Fisher problem. It refers to the case of two samples 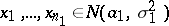 and
and 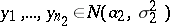 having equal size,
having equal size, 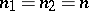 . The critical regions are given by the inequality
. The critical regions are given by the inequality
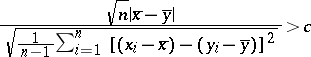 |
for some constant 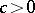 , where
, where
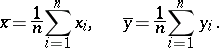 |
The left-hand side of the inequality has a Student distribution with 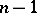 degrees of freedom, connecting the significance level of the test to the constant
degrees of freedom, connecting the significance level of the test to the constant  . Bartlett's test is a special case of the Scheffe test and has analogous extremal properties, but was presented by M.S. Bartlett [1] prior to this solution. A second test of Bartlett is connected with the comparison of the variances of many samples.
. Bartlett's test is a special case of the Scheffe test and has analogous extremal properties, but was presented by M.S. Bartlett [1] prior to this solution. A second test of Bartlett is connected with the comparison of the variances of many samples.
References
| [1] | M.S. Bartlett, "The information available in small samples" Proc. Cambridge Philos. Soc. (1) , 32 : 3 (1936) pp. 560–566 |
How to Cite This Entry:
Bartlett test. O.V. Shalaevskii (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bartlett_test&oldid=15637
Bartlett test. O.V. Shalaevskii (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bartlett_test&oldid=15637
This text originally appeared in Encyclopedia of Mathematics - ISBN 1402006098