Barrier

Lebesgue barrier, in potential theory

A function the existence of which is a necessary and sufficient condition for the regularity of a boundary point with respect to the behaviour of a generalized solution of the Dirichlet problem at that point (cf. Perron method; Regular boundary point).

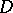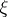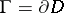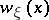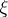Let be a domain in a Euclidean space , , and let be a point on its boundary . A barrier for the point is any function , continuous in the intersection of the closed domain with some ball with centre at , which is superharmonic in 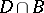and positive in 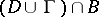, except at 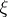, at which it vanishes. For instance, if 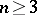and 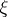is any boundary point for which there exists a closed ball 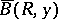in 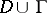which meets 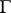only in 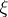, one can take as a barrier the harmonic function

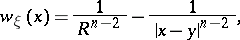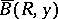where is the radius of and 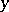is its centre.

A barrier in the theory of functions of (several) complex variables is a function the existence of which for all boundary points of the domain 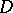implies that 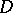is a domain of holomorphy. Let 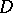be a domain in the complex space 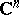, , 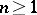and let 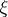be a point of the boundary 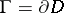. Any analytic functio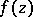n in 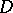with a singular point at 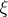will then be a barrier at 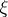. Thus, the function 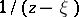is a barrier for the boundary point of any plane domain . 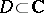There also exists a barrier at any point 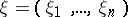of the boundary of the ball

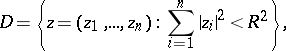e.g. the function .

A barrier exists at a boundary point 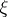of a domain 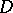if there is an analytic function defined in 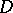that is unbounded at 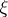, i.e. is such that for some sequence of points 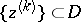which converges to 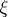one has:

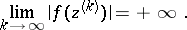The converse is true for domains 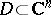in the following strong form: For any set 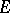of boundary points of a domain 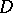at which a barrier exists, one can find a function holomorphic in 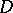which is unbounded at all points o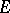f . If 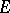is everywhere dense in the boundary of 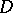, then 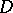is a domain of holomorphy.

References

[1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) MR0195654
[2]	V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) pp. Chapt. 3 (Translated from Russian)
[3]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) pp. Chapt. 3 (In Russian) Zbl 0578.32001 Zbl 0574.30001

Comments

Good English references for the Lebesgue barrier are [a1] and [a2].

References

[a1]	W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Cambridge Univ. Press (1976) MR0460672 MR0419791 MR0412442 MR0442324 Zbl 0419.31001 Zbl 0339.31003 Zbl 0328.33011
[a2]	L.L. Helms, "Introduction to potential theory" , Acad. Press (1975) (Translated from German) MR0460666 Zbl 0188.17203