Bar induction
An inductive way of reasoning, used in intuitionistic mathematics (cf. Intuitionism), which may be described as follows. Let certain properties  and
and  be defined on finite tuples (cf. Tuple) of natural integers, such that 1) the property
be defined on finite tuples (cf. Tuple) of natural integers, such that 1) the property  is decidable, i.e. it is possible to effectively find out whether it is fulfilled on any tuple
is decidable, i.e. it is possible to effectively find out whether it is fulfilled on any tuple  or not; 2) for any choice sequence
or not; 2) for any choice sequence  it is possible to find a tuple of the form
it is possible to find a tuple of the form  for which
for which  is fulfilled. Moreover, if 2) is fulfilled, one says that
is fulfilled. Moreover, if 2) is fulfilled, one says that  "bars" the empty tuple
"bars" the empty tuple  (hence the name); 3) for any tuple
(hence the name); 3) for any tuple 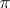 of natural integers, if
of natural integers, if 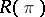 , then
, then 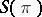 (the so-called basis of the bar induction); and 4) if
(the so-called basis of the bar induction); and 4) if 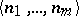 is a tuple such that for any natural number
is a tuple such that for any natural number  one has
one has 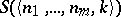 , then
, then 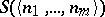 ; this property is known as the step of the bar induction.
; this property is known as the step of the bar induction.
If the conditions 1) through 4) above are met, one can deduce from the principle of bar induction that 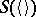 .
.
The use of bar induction was proposed by L.E.J. Brouwer as an intuitionistic method of reasoning which indicates that the collection of free choice sequences is incomplete and to some extent uncountable. It was demonstrated, in particular, by S.C. Kleene and, independently, by A.A. Markov that it follows from the principle of bar induction (in fact, even from a corollary of bar induction, the fan theorem) that not all choice sequences are recursive (cf. Fan).
The forms of bar induction which one started to utilize in the foundations of mathematics in the 1960's do not deal with tuples of natural numbers, but rather with tuples of more complex objects, such as tuples of choice sequences.
Bar induction can be written down in the language of formal intuitionistic mathematical analysis as follows:
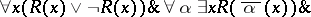 |
 |
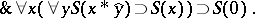 |
References
| [1] | S.C. Kleene, R.E. Vesley, "The foundations of intuitionistic mathematics: especially in relation to recursive functions" , North-Holland (1965) |
Comments
References
| [a1] | M.A.E. Dummett, "Elements of intuitionism" , Clarendon Press (1977) |
| [a2] | A.S. Troelstra, "Choice sequences" , Clarendon Press (1977) |
Bar induction. A.G. Dragalin (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bar_induction&oldid=12849