Banach-Saks property
A Banach space 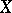 is said to have the Banach–Saks property if bounded sequences admit subsequences having norm-convergent arithmetic means (such subsequences are called Banach–Saks sequences). The origin of the Banach–Saks property can be traced back to a result of S. Mazur: If a sequence
is said to have the Banach–Saks property if bounded sequences admit subsequences having norm-convergent arithmetic means (such subsequences are called Banach–Saks sequences). The origin of the Banach–Saks property can be traced back to a result of S. Mazur: If a sequence  in a Banach space
in a Banach space  is weakly convergent to some point
is weakly convergent to some point  , then there is a sequence formed by convex combinations of
, then there is a sequence formed by convex combinations of  that converges in norm to
that converges in norm to  . (The proof is just an application of the Hahn–Banach theorem:
. (The proof is just an application of the Hahn–Banach theorem:  belongs by hypothesis to the weak closure of the convex hull of the sequence, and the convex closed sets coincide for the weak and norm topologies.) It is then a natural question to ask if that convex combination can be chosen to be the arithmetic means. S. Banach and S. Saks [a1] proved that this is the case in
belongs by hypothesis to the weak closure of the convex hull of the sequence, and the convex closed sets coincide for the weak and norm topologies.) It is then a natural question to ask if that convex combination can be chosen to be the arithmetic means. S. Banach and S. Saks [a1] proved that this is the case in 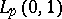 ,
, 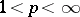 . S. Kakutani [a8] extended this result to uniformly convex spaces. Later, T. Nishiura and D. Waterman [a9] proved that a space with the Banach–Saks property must be reflexive (cf. Reflexive space) and W. Schlenk [a13] proved that
. S. Kakutani [a8] extended this result to uniformly convex spaces. Later, T. Nishiura and D. Waterman [a9] proved that a space with the Banach–Saks property must be reflexive (cf. Reflexive space) and W. Schlenk [a13] proved that 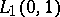 satisfies the weak Banach–Saks property: weakly null (instead of bounded) sequences have Banach–Saks subsequences. J. Schreier [a12] showed that a certain weakly null sequence of indicator functions on the compact space
satisfies the weak Banach–Saks property: weakly null (instead of bounded) sequences have Banach–Saks subsequences. J. Schreier [a12] showed that a certain weakly null sequence of indicator functions on the compact space  contains no Banach–Saks subsequences; thus, not all spaces have the weak Banach–Saks property. An example of A. Baernstein II [a5] shows that not all reflexive spaces have the Banach–Saks property.
contains no Banach–Saks subsequences; thus, not all spaces have the weak Banach–Saks property. An example of A. Baernstein II [a5] shows that not all reflexive spaces have the Banach–Saks property.
Subsequences of Banach–Saks sequences need not be Banach–Saks. For example, consider a sequence formed by an infinity of zeros and ones. The so-called Ramsey methods have had a great impact in the study of the Banach–Saks property and, in general, of properties depending on the extraction of subsequences, because they introduce some order into this phenomenon. The basic Ramsey theorem asserts that given a sequence and a property 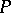 that pairs may have, either there is a subsequence for which all pairs have
that pairs may have, either there is a subsequence for which all pairs have 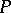 or there is a subsequence for which no pair has
or there is a subsequence for which no pair has 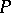 . Some topological work allows one to replace, in some cases, "pair" by "subsequence" . For instance, a bounded sequence in a Banach space either contains a subsequence such that all its further subsequences are Banach–Saks or it contains a subsequence having no Banach–Saks subsequences. Classical, as well as Ramsey, methods are described in full detail in [a4]; a survey of counterexamples and new related properties is [a3].
. Some topological work allows one to replace, in some cases, "pair" by "subsequence" . For instance, a bounded sequence in a Banach space either contains a subsequence such that all its further subsequences are Banach–Saks or it contains a subsequence having no Banach–Saks subsequences. Classical, as well as Ramsey, methods are described in full detail in [a4]; a survey of counterexamples and new related properties is [a3].
Regarding stability properties, J.R. Partington [a10] proved that the Banach–Saks property is stable under 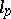 -sums, and W. Schachermayer [a11] and J. Bourgain (see [a7]) examples of Banach spaces
-sums, and W. Schachermayer [a11] and J. Bourgain (see [a7]) examples of Banach spaces 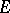 with the Banach–Saks property but for which
with the Banach–Saks property but for which 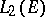 does not have the Banach–Saks property. B. Beauzamy [a6] studied the behaviour of the Banach–Saks property under interpolation. It does not pass from
does not have the Banach–Saks property. B. Beauzamy [a6] studied the behaviour of the Banach–Saks property under interpolation. It does not pass from  to
to 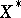 (or vice versa). It is unknown what the dual of a space with the Banach–Saks property looks like.
(or vice versa). It is unknown what the dual of a space with the Banach–Saks property looks like.
References
| [a1] | S. Banach, S. Saks, "Sur la convergence forte dans les champs 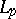 " Studia Math. , 2 (1930) pp. 51–57 " Studia Math. , 2 (1930) pp. 51–57 |
| [a2] | B. Beauzamy, J.-T. Lapresté, "Modèles étalés des espaces de Banach" , Hermann (1984) |
| [a3] | J.M.F. Castillo, "Extraction of subsequences in Banach spaces" Extracta Math. , 7 (1992) pp. 77–88 |
| [a4] | J. Diestel, "Sequences and series in Banach spaces" , GTM , 92 , Springer (1984) |
| [a5] | A. Baernstein II, "On reflexivity and summability" Studia Math. , 42 (1972) pp. 91–94 |
| [a6] | B. Beauzamy, "Espaces d'interpolation réels: topologie et géométrie" , Lecture Notes in Mathematics , 666 , Springer (1978) |
| [a7] | S. Guerre, "La propriété de Banach–Saks ne pase pas de 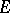 à à 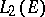 , d'áprés J. Bourgin" Sem. Anal. Fonctionnelle Ecole Polytechn. Palaiseau (1979–1980) pp. Exp. 8 , d'áprés J. Bourgin" Sem. Anal. Fonctionnelle Ecole Polytechn. Palaiseau (1979–1980) pp. Exp. 8 |
| [a8] | S. Kakutani, "Weak convergence in uniformly convex spaces" Math. Inst. Osaka Imp. Univ. (1938) pp. 165–167 |
| [a9] | T. Nishiura, D. Waterman, "Reflexivity and summability" Studia Math. , 23 (1963) pp. 53–57 |
| [a10] | J.R. Partington, "On the Banach–Saks property" Math. Proc. Cambridge Philos. Soc. , 82 (1977) pp. 369–374 |
| [a11] | W. Schachermayer, "The Banach–Saks property is not 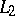 -hereditary" Israel J. Math. , 40 (1981) pp. 340–344 -hereditary" Israel J. Math. , 40 (1981) pp. 340–344 |
| [a12] | J. Schreier, "Ein Gegenbeispiel zur Theorie der swachen Konvergenz" Studia Math. , 2 (1930) pp. 58–62 |
| [a13] | W. Schlenk, "Sur les suites faiblement convergents dans l'espace 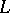 " Studia Math. , 25 (1969) pp. 337–341 " Studia Math. , 25 (1969) pp. 337–341 |
Banach-Saks property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banach-Saks_property&oldid=22059