Ball

A set of points in a Euclidean space at a distance from a given point (the centre of the ball) less than (an open ball ), or not greater than (a closed ball ) a quantity (the radius of the ball), i.e.

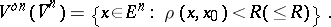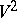A ball is a line segment, is a disc, for is sometimes called a hyperball. The boundary (surface) of a ball is a sphere.

The volume of a ball is

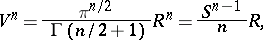where 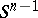is the surface of the boundary sphere and 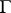is the gamma-function: 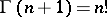, 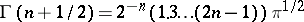. In particular,

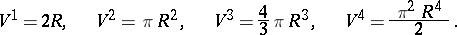With the increase of the dimension, the volume of a ball "concentrates" at its surface:

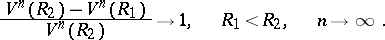A ball is the simplest geometrical figure. Its topology is trivial. Among all bodies of an equal volume, a ball has minimal surface, and among all bodies of an equal surface, it has maximal volume.

In exactly the same manner a ball can be defined in a metric space; however, in this case it need not be, for example, strictly convex, its surface may have non-smooth points, etc., that is, it may have all phenomena characteristic of arbitrary convex bodies.

Unlike a finite-dimensional ball, an infinite-dimensional ball, being the direct limit of a sequence of balls of successive dimensions imbedded in one another, does not have a compact closure. On the contrary, the compactness of a ball in a topological vector space indicates the finite dimensionality of the latter.

For references, see Sphere.