Zolotarev polynomials
Zolotareff polynomials, Solotareff polynomials
For each  , the Zolotarev polynomial
, the Zolotarev polynomial  is the unique solution of the problem
is the unique solution of the problem
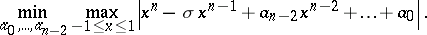 |
That is, the Zolotarev polynomials of degree  are the polynomials whose leading two coefficients are fixed, and that deviate least from zero on the interval
are the polynomials whose leading two coefficients are fixed, and that deviate least from zero on the interval  , in the uniform norm (cf. also Uniform approximation; Polynomial least deviating from zero).
, in the uniform norm (cf. also Uniform approximation; Polynomial least deviating from zero).
This problem was formulated and solved by E.I. Zolotarev. It is the first of four Zolotarev problems in approximation theory. Zolotarev's second problem asks for the monic polynomial  of degree
of degree  that deviates least from zero on the interval
that deviates least from zero on the interval  while satisfying the extra condition
while satisfying the extra condition  for some
for some 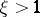 and
and 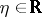 . The class of solutions (dependent on
. The class of solutions (dependent on 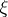 and
and 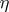 ) are normalized Zolotarev polynomials. The third and fourth problems of Zolotarev deal with rational functions.
) are normalized Zolotarev polynomials. The third and fourth problems of Zolotarev deal with rational functions.
In each of these problems the influence of P.L. Chebyshev can be seen, whose lectures Zolotarev attended, as these problems are all generalizations of problems of Chebyshev. 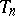 , the monic Chebyshev polynomial of degree
, the monic Chebyshev polynomial of degree  , solves problem one but without any restriction on the coefficient of
, solves problem one but without any restriction on the coefficient of 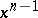 , cf. Chebyshev polynomials. (From symmetry considerations,
, cf. Chebyshev polynomials. (From symmetry considerations,  .)
.)
It follows from the equi-oscillation theorem in the theory of best uniform approximation that 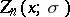 is uniquely determined by the fact that the coefficients of
is uniquely determined by the fact that the coefficients of 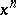 and
and  are as given, and it attains its norm, alternately in sign, at least
are as given, and it attains its norm, alternately in sign, at least  times in
times in 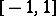 . Thus it is easily verified that for
. Thus it is easily verified that for 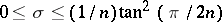 ,
,
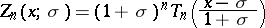 |
(which is what one gets when the Chebyshev polynomial is fixed at 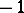 and pulled to the right as long as the resulting polynomial attains its norm alternately at
and pulled to the right as long as the resulting polynomial attains its norm alternately at  points in
points in 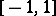 ). For
). For 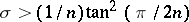 the Zolotarev polynomial is given in terms of elliptic integrals, see e.g. [a1], [a4], [a6], [a3] for more details. It suffices to consider
the Zolotarev polynomial is given in terms of elliptic integrals, see e.g. [a1], [a4], [a6], [a3] for more details. It suffices to consider  , since
, since 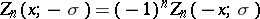 .
.
Zolotarev polynomials, suitably normalized, are also the class of extremal polynomials in the pointwise Markov inequalities, cf. Markov inequality. That is, they maximize
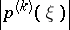 |
for fixed 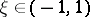 and
and  , over all polynomials of degree at most
, over all polynomials of degree at most  which are bounded by
which are bounded by 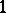 on
on 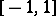 . (For
. (For 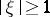 the extremal polynomial is always the Chebyshev polynomial.) This problem is considered in detail in [a9] (see especially the index).
the extremal polynomial is always the Chebyshev polynomial.) This problem is considered in detail in [a9] (see especially the index).
Various generalizations of Zolotarev polynomials can be found in the literature. The problem of finding the extremal polynomials when  coefficients, rather than just
coefficients, rather than just  coefficients, are fixed was considered by A. Akhiezer and by N.N. Meiman. For a generalization of the first Zolotarev problem to different (symmetric) domains and
coefficients, are fixed was considered by A. Akhiezer and by N.N. Meiman. For a generalization of the first Zolotarev problem to different (symmetric) domains and 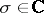 , see [a7] and references therein. Zolotarev perfect splines and Zolotarev
, see [a7] and references therein. Zolotarev perfect splines and Zolotarev 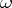 -polynomials were introduced when generalizing the pointwise Markov inequalities to other spaces of functions, see e.g. [a5], [a8], and [a2].
-polynomials were introduced when generalizing the pointwise Markov inequalities to other spaces of functions, see e.g. [a5], [a8], and [a2].
Due to fashions in transliteration, Zolotarev's name is sometimes written as Zolotareff or Solotareff.
References
| [a1] | A. Achieser, "Theory of approximation" , F. Ungar (1956) (In Russian) |
| [a2] | S.K. Bagdasarov, "Zolotarev 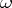 -polynomials in -polynomials in 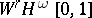 " J. Approx. Th. , 90 (1997) pp. 340–378 " J. Approx. Th. , 90 (1997) pp. 340–378 |
| [a3] | B.C. Carlson, J. Todd, "Zolotarev's first problem: the best approximation by polynomials of degree 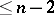 to to 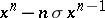 in in 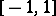 " Aequat. Math. , 26 (1983) pp. 1–33 " Aequat. Math. , 26 (1983) pp. 1–33 |
| [a4] | P. Erdős, G. Szegő, "On a problem of I. Schur" Ann. Math. , 43 (1942) pp. 451–470 (Correction: 74 (1961), 628; Reprinted in G. Szegő, Collected Papers (R.A. Askey, ed.), Vol. 2 (1982), 807-827, Birkhäuser) |
| [a5] | S. Karlin, "Oscillatory perfect splines and related extremal problems" S. Karlin (ed.) C.A. Micchelli (ed.) A. Pinkus (ed.) I.J. Schoenberg (ed.) , Spline Functions and Approximation Theory , Acad. Press (1976) pp. 371–460 |
| [a6] | S. Paszkowski, "The theory of uniform approximation I. Non-asymptotic theoretical problems" Rozp. Mat. , 26 (1962) |
| [a7] | F. Peherstorfer, K. Schiefermayr, "Explicit generalized Zolotarev polynomials with complex coefficients II" East J. Approx. , 3 (1997) pp. 473–483 |
| [a8] | A. Pinkus, "Some extremal properties of perfect splines and the pointwise Landau problem on the finite interval" J. Approx. Th. , 23 (1978) pp. 37–64 |
| [a9] | E.V. Voronovskaja, "The functional method and its applications" Transl. Math. Monographs , 28 (1970) |
Zolotarev polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zolotarev_polynomials&oldid=11923