Zassenhaus conjecture
Just as the only roots of unity in a cyclotomic field 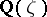 are of the form
are of the form 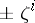 , there is the classical theorem of G. Higman stating that the torsion units in the integral group ring
, there is the classical theorem of G. Higman stating that the torsion units in the integral group ring 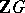 of a finite Abelian group are of the form
of a finite Abelian group are of the form 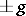 ,
, 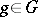 . Of course, if
. Of course, if 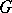 is non-Abelian, then any conjugate of
is non-Abelian, then any conjugate of 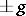 is also of finite order; however, these are not all the torsion units in
is also of finite order; however, these are not all the torsion units in 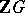 . The famous Zassenhaus conjecture says that for a finite group
. The famous Zassenhaus conjecture says that for a finite group 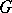 all torsion units of
all torsion units of 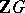 are rationally conjugate to
are rationally conjugate to 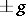 ,
, 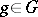 :
:
ZC1) Let 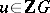 ,
, 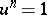 for some
for some  ; then
; then 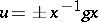 for some
for some 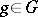 and some unit
and some unit 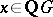 . This conjecture was proved to be true by A. Weiss, first for
. This conjecture was proved to be true by A. Weiss, first for 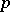 -groups [a16] and then for nilpotent groups [a17] (cf. also Nilpotent group). In fact, Weiss proved the following stronger Zassenhaus conjecture for nilpotent groups:
-groups [a16] and then for nilpotent groups [a17] (cf. also Nilpotent group). In fact, Weiss proved the following stronger Zassenhaus conjecture for nilpotent groups:
ZC3) If 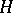 is a finite subgroup of units of augmentation one in
is a finite subgroup of units of augmentation one in  , then there exists a unit
, then there exists a unit 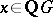 such that
such that 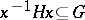 . A special case of this is the following conjecture:
. A special case of this is the following conjecture:
ZC2) If 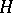 is a subgroup of
is a subgroup of  of augmentation one of order
of augmentation one of order 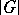 such that
such that  , then there exists a unit
, then there exists a unit 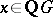 with
with  . This last conjecture was earlier proved by K. Roggenkamp and L.R. Scott [a12] for nilpotent groups. Subsequently, they also gave a counterexample to ZC2) (unpublished), which appears in a modified form in [a5].
. This last conjecture was earlier proved by K. Roggenkamp and L.R. Scott [a12] for nilpotent groups. Subsequently, they also gave a counterexample to ZC2) (unpublished), which appears in a modified form in [a5].
Clearly, ZC3) implies ZC1) and ZC2). Also, ZC2) implies that if two group rings 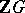 and
and 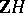 are isomorphic, then the groups
are isomorphic, then the groups 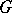 and
and 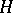 are isomorphic. This isomorphism problem was proposed in [a3]:
are isomorphic. This isomorphism problem was proposed in [a3]:
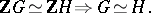 | (a1) |
Of course, then, (a1) is true for nilpotent groups. Moreover, it was proved by A. Whitcomb [a18] that (a1) is true for metabelian groups. M. Hertweck [a2] has given a counterexample to (a1).
Conjecture ZC1) is open in general (as of 2000). Besides nilpotent groups, it is known to be true for certain split metacyclic groups [a10]: If  is the semi-direct product of two cyclic groups
is the semi-direct product of two cyclic groups 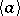 and
and 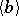 of relative prime orders, then ZC1) holds for
of relative prime orders, then ZC1) holds for  .
.
This result has been strengthened to ZC3) [a15].
There are several useful and interesting extensions of the above conjectures. Suppose that 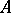 is a normal subgroup of index
is a normal subgroup of index  in
in 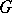 . Then
. Then 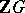 can be represented by
can be represented by  -matrices over
-matrices over 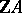 . Any torsion unit
. Any torsion unit  of
of 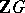 that is mapped by the natural homomorphism
that is mapped by the natural homomorphism 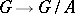 to
to 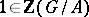 gives rise to a torsion matrix
gives rise to a torsion matrix 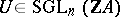 . Here,
. Here, 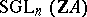 denotes the subgroup of the general linear group
denotes the subgroup of the general linear group 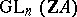 consisting of the matrices
consisting of the matrices 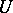 that are mapped by the augmentation homomorphism
that are mapped by the augmentation homomorphism  , when applied to each entry, to the identity matrix. Thus, ZC1) translates to the question about diagonalization of
, when applied to each entry, to the identity matrix. Thus, ZC1) translates to the question about diagonalization of 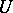 in
in 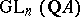 : Is a torsion matrix
: Is a torsion matrix 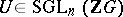 , where
, where 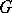 is a finite group, conjugate in
is a finite group, conjugate in 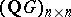 to a matrix of the form
to a matrix of the form 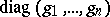 ,
,  ?
?
This was answered positively in [a16] for 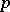 -groups (cf. also
-groups (cf. also 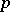 -group). See [a1] for an explicit example of a matrix
-group). See [a1] for an explicit example of a matrix 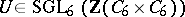 that cannot be diagonalized but for which
that cannot be diagonalized but for which 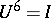 . Such a matrix
. Such a matrix 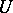 exists for a finite nilpotent group
exists for a finite nilpotent group 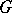 and some
and some  if and only if
if and only if 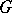 has at least two non-cyclic Sylow
has at least two non-cyclic Sylow 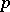 -subgroups [a1] (cf. also Sylow subgroup).
-subgroups [a1] (cf. also Sylow subgroup).
However, it was proved in [a6] that if 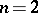 and
and 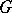 is finite Abelian, then
is finite Abelian, then 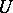 is conjugate in
is conjugate in 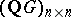 to
to  . This has been extended to
. This has been extended to 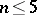 in [a8], bridging the gap between
in [a8], bridging the gap between  and
and 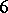 .
.
The Zassenhaus conjectures and the isomorphism problem have also been studied for infinite groups 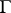 . The statements remain the same and the group
. The statements remain the same and the group 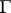 is arbitrary. A counterexample to ZC1) was provided in [a9]. Conjecture ZC2) also does not hold for infinite groups, as shown by S.K. Sehgal and A.E. Zalesskii (see [a14], p. 279).
is arbitrary. A counterexample to ZC1) was provided in [a9]. Conjecture ZC2) also does not hold for infinite groups, as shown by S.K. Sehgal and A.E. Zalesskii (see [a14], p. 279).
However, one can ask if any torsion unit 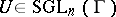 can be stably diagonalized to
can be stably diagonalized to 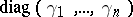 ,
, 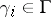 . This has been proved [a7] to be true for
. This has been proved [a7] to be true for 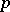 -elements
-elements 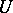 when
when 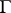 is nilpotent. The isomorphism problem also has a positive answer for finitely-generated nilpotent groups of class
is nilpotent. The isomorphism problem also has a positive answer for finitely-generated nilpotent groups of class  , cf. [a11]. In general for nilpotent groups the problem remains open (as of 2000).
, cf. [a11]. In general for nilpotent groups the problem remains open (as of 2000).
References
| [a1] | G. Cliff, A. Weiss, "Finite groups of matrices over group rings" Trans. Amer. Math. Soc. , 352 (2000) pp. 457–475 |
| [a2] | M. Hertweck, "A solution of the isomorphism problem for integral group rings" (to appear) |
| [a3] | G. Higman, "Units in group rings" , D. Phil. Thesis Univ. Oxford (1940) |
| [a4] | G. Higman, "The units of group rings" Proc. London Math. Soc. , 46 (1940) pp. 231–248 |
| [a5] | L. Klingler, "Construction of a counterexample to a conjecture of Zassenhaus" Commun. Algebra , 19 (1991) pp. 2303–2330 |
| [a6] | I.S. Luthar, I.B.S. Passi, "Torsion units in matrix group rings" Commun. Algebra , 20 (1992) pp. 1223–1228 |
| [a7] | Z. Marciniak, S.K. Sehgal, "Finite matrix groups over nilpotent group rings" J. Algebra , 181 (1996) pp. 565–583 |
| [a8] | Z. Marciniak, S.K. Sehgal, "Torsion matrices over abelian group rings" J. Group Th. , 3 (2000) pp. 67–75 |
| [a9] | Z. Marciniak, S.K. Sehgal, "Zassenhaus conjecture and infinite nilpotent groups" J. Algebra , 184 (1996) pp. 207–212 |
| [a10] | C. Polcino Milies, J. Ritter, S.K. Sehgal, "On a conjecture of Zassenhaus on torsion units in integral group rings, II" Proc. Amer. Math. Soc. , 97 (1986) pp. 201–206 |
| [a11] | J. Ritter, S.K. Sehgal, "Isomorphism of group rings" Archiv Math. , 40 (1983) pp. 32–39 |
| [a12] | K. Roggenkamp, L. Scott, "Isomorphisms for 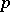 -adic group rings" Ann. Math. , 126 (1987) pp. 593–647 -adic group rings" Ann. Math. , 126 (1987) pp. 593–647 |
| [a13] | S.K. Sehgal, "Topics in group rings" , M. Dekker (1978) |
| [a14] | S.K. Sehgal, "Units in integral group rings" , Longman (1993) |
| [a15] | A. Valenti, "Torsion units in integral group rings" Proc. Amer. Math. Soc. , 120 (1994) pp. 1–4 |
| [a16] | A. Weiss, "Rigidity of 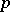 -adic -adic  -torsion" Ann. of Math. , 127 (1988) pp. 317–332 -torsion" Ann. of Math. , 127 (1988) pp. 317–332 |
| [a17] | A. Weiss, "Torsion units in integral group rings" J. Reine Angew. Math. , 415 (1991) pp. 175–187 |
| [a18] | A. Whitcomb, "The group ring problem" PhD Thesis Univ. Chicago (1968) |
Zassenhaus conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zassenhaus_conjecture&oldid=11419