Weyl correspondence
A mapping between a class of (generalized) functions on the phase space  and the set of closed densely defined operators on the Hilbert space
and the set of closed densely defined operators on the Hilbert space  [a1] (cf. also Generalized function; Hilbert space). It is defined as follows: Let
[a1] (cf. also Generalized function; Hilbert space). It is defined as follows: Let  be an arbitrary point of
be an arbitrary point of  (called phase space) and let
(called phase space) and let  be an arbitrary vector on
be an arbitrary vector on  . For a point in
. For a point in  , the Grossmann–Royer operator
, the Grossmann–Royer operator  is defined as [a2], [a3]:
is defined as [a2], [a3]:
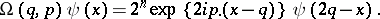 |
Now, take a function 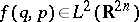 . The Weyl mapping
. The Weyl mapping 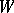 is defined as [a4], [a5]:
is defined as [a4], [a5]:
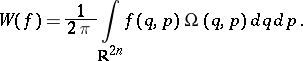 |
The Weyl mapping defines the Weyl correspondence between functions and operators. It has the following properties:
i) It is linear and one-to-one.
ii) If 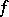 is bounded, the operator
is bounded, the operator 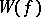 is also bounded.
is also bounded.
iii) If 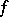 is real,
is real, 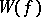 is self-adjoint (cf. also Self-adjoint operator).
is self-adjoint (cf. also Self-adjoint operator).
iv) Let 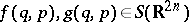 , the Schwartz space, and define the Weyl product as [a6]:
, the Schwartz space, and define the Weyl product as [a6]:
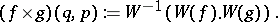 |
The Weyl product defines an algebra structure on 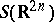 , which admits a closure
, which admits a closure 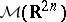 with the topology of the space of tempered distributions,
with the topology of the space of tempered distributions, 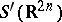 (cf. also Generalized functions, space of). The algebra
(cf. also Generalized functions, space of). The algebra 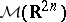 includes the space
includes the space 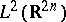 and the Weyl mapping can be uniquely extended to
and the Weyl mapping can be uniquely extended to 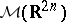 .
.
v) Obviously,  .
.
vi) If 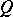 is the multiplication operator on
is the multiplication operator on  and
and 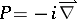 , then
, then 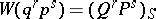 , where
, where 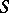 denotes the symmetric product of
denotes the symmetric product of  factors
factors 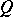 and
and  factors
factors 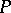 .
.
vii) For any positive trace-class operator 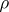 on
on  , there exists a signed measure
, there exists a signed measure 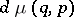 on
on  , such that for any
, such that for any 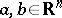 ,
,
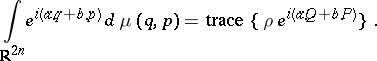 |
This measure has a Radon–Nikodým derivative (cf. also Radon–Nikodým theorem) with respect to the Lebesgue measure, which is called the Wigner function associated to 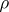 .
.
The Weyl correspondence is used by physicists to formulate quantum mechanics of non-relativistic systems without spin or other constraints on the flat phase space  [a5].
[a5].
The Stratonovich–Weyl correspondence [a4], [a5], [a7] or Stratonovich–Weyl mapping generalizes the Weyl mapping to other types of phase spaces. Choose a co-adjoint orbit 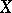 of the representation group
of the representation group 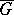 of a certain Lie group
of a certain Lie group 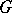 of symmetries of a given physical system as phase space. The Hilbert space
of symmetries of a given physical system as phase space. The Hilbert space 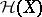 used here supports a linear unitary irreducible representation of the group
used here supports a linear unitary irreducible representation of the group 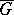 associated to
associated to 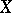 . Then, a generalization of the Grossmann–Royer operator is needed, associating each point
. Then, a generalization of the Grossmann–Royer operator is needed, associating each point  of the orbit
of the orbit 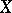 with a self-adjoint operator
with a self-adjoint operator 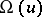 . Then, for a suitable class of measurable functions
. Then, for a suitable class of measurable functions 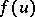 on
on 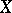 , one defines:
, one defines:  , where
, where 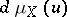 is a measure on
is a measure on 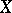 that is invariant under the action of
that is invariant under the action of 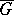 ; such a measure is uniquely defined, up to a multiplicative constant.
; such a measure is uniquely defined, up to a multiplicative constant.
The Weyl correspondence is a particular case of the Stratonovich–Weyl correspondence for which 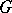 is the Heisenberg group, [a1], [a5].
is the Heisenberg group, [a1], [a5].
References
| [a1] | H. Weyl, "The theory of groups and quantum mechanics" , Dover (1931) |
| [a2] | A. Grossmann, "Parity operator and quantization of 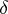 functions" Comm. Math. Phys. , 48 (1976) pp. 191 functions" Comm. Math. Phys. , 48 (1976) pp. 191 |
| [a3] | A. Royer, "Wigner function as the expectation value of a parity operator" Phys. Rev. A , 15 (1977) pp. 449 |
| [a4] | J.M. Gracia-Bondia, J.C. Varilly, "The Moyal representation of spin" Ann. Phys. (NY) , 190 (1989) pp. 107 |
| [a5] | M. Gadella, "Moyal formulation of quantum mechanics" Fortschr. Phys. , 43 (1995) pp. 229 |
| [a6] | J.M. Gracia-Bondia, J.C. Varilly, "Algebras of distributions suitable for phase space quantum mechanics" J. Math. Phys. , 29 (1988) pp. 869 |
| [a7] | J.C. Varilly, "The Stratonovich–Weyl correspondence: a general approach to Wigner functions" BIBOS preprint 345 Univ. Bielefeld, Germany (1988) |
Weyl correspondence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weyl_correspondence&oldid=18852