Weingarten surface
A surface whose mean curvature is in functional relationship with its Gaussian curvature. A necessary and sufficient condition for a surface 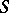 to be a Weingarten surface is for both sheets of its focal set to be superimposed on a surface of revolution, and for the edges of regression (cuspidal edges) of the normals to the lines of curvature of
to be a Weingarten surface is for both sheets of its focal set to be superimposed on a surface of revolution, and for the edges of regression (cuspidal edges) of the normals to the lines of curvature of 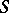 to be superimposed on the meridians. Examples of Weingarten surfaces include surfaces of revolution and surfaces of constant mean or constant Gaussian curvature. Introduced by J. Weingarten [1], [2] in the context of the problem of finding all surfaces isometric to a given surface of revolution. The latter problem can be reduced to finding all Weingarten surfaces of this class.
to be superimposed on the meridians. Examples of Weingarten surfaces include surfaces of revolution and surfaces of constant mean or constant Gaussian curvature. Introduced by J. Weingarten [1], [2] in the context of the problem of finding all surfaces isometric to a given surface of revolution. The latter problem can be reduced to finding all Weingarten surfaces of this class.
References
| [1] | J. Weingarten, "Ueber eine Klasse auf einander abwickelbarer Flächen" J. Reine Angew. Math. , 59 (1861) pp. 382–393 |
| [2] | J. Weingarten, "Ueber die Flächen, derer Normalen eine gegebene Fläche berühren" J. Reine Angew. Math. , 62 (1863) pp. 61–63 |
| [3] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
References
| [a1] | D.J. Struik, "Lectures on classical differential geometry" , Addison-Wesley (1950) |
Weingarten surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weingarten_surface&oldid=12641