Weight function
The weight 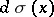 of a system of orthogonal polynomials
of a system of orthogonal polynomials 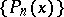 . If
. If 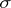 is a non-decreasing bounded function on an interval
is a non-decreasing bounded function on an interval 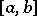 with infinitely many points of growth, then the measure
with infinitely many points of growth, then the measure 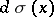 , called a weight function, uniquely defines a system of polynomials
, called a weight function, uniquely defines a system of polynomials 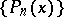 , having positive leading coefficients and satisfying the orthonormality condition.
, having positive leading coefficients and satisfying the orthonormality condition.
The distribution function, or integral weight, 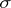 can be represented in the form
can be represented in the form
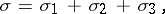 |
where 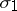 is an absolutely-continuous function, called the kernel,
is an absolutely-continuous function, called the kernel, 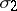 is the continuous singular component and
is the continuous singular component and 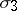 is the jump function. If
is the jump function. If 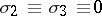 , then one can make the substitution
, then one can make the substitution 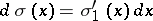 under the integral sign; here the derivative
under the integral sign; here the derivative 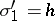 is called the differential weight of the system of polynomials.
is called the differential weight of the system of polynomials.
Of the three components of the distribution function, only the kernel 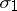 affects the asymptotic properties of the orthogonal polynomials.
affects the asymptotic properties of the orthogonal polynomials.
For references see Orthogonal polynomials.
Comments
The term "weight function" is often exclusively used for what is called here "differential weight" .
Weight function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weight_function&oldid=12399