Weierstrass formula
for the increment of a functional
A formula in the classical calculus of variations (cf. Variational calculus), defining the values of the functional
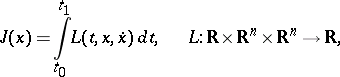 |
in the form of a curvilinear integral of the Weierstrass 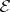 -function. Let the vector function
-function. Let the vector function 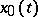 be an extremal of the functional
be an extremal of the functional 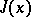 , and let it be included in an extremal field with vector-valued field slope function
, and let it be included in an extremal field with vector-valued field slope function 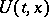 and action
and action 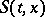 , corresponding to this field (cf. Hilbert invariant integral). Weierstrass' formula
, corresponding to this field (cf. Hilbert invariant integral). Weierstrass' formula
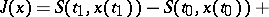 | (1) |
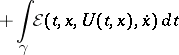 |
applies to any curve 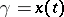 in the domain covered by the field. In particular, if the boundary conditions of the curves
in the domain covered by the field. In particular, if the boundary conditions of the curves 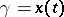 and
and 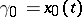 are identical, i.e. if
are identical, i.e. if 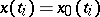 ,
, 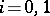 , one obtains Weierstrass' formula for the increment of a functional:
, one obtains Weierstrass' formula for the increment of a functional:
 | (2) |
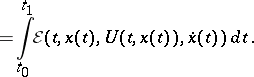 |
Formulas (1) and (2) are sometimes referred to as Weierstrass' fundamental theorem.
References
| [1] | C. Carathéodory, "Calculus of variations and partial differential equations of the first order" , 1–2 , Holden-Day (1965–1967) (Translated from German) |
| [2] | L. Young, "Lectures on the calculus of variations and optimal control theory" , Saunders (1969) |
| [3] | N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian) |
Weierstrass formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_formula&oldid=16280