Weierstrass conditions (for a variational extremum)
Necessary and (partially) sufficient conditions for a strong extremum in the classical calculus of variations (cf. Variational calculus). Proposed in 1879 by K. Weierstrass.
Weierstrass' necessary condition: For the functional
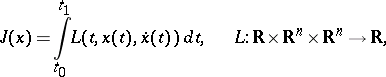 |
to attain a strong local minimum on the extremal 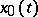 , it is necessary that the inequality
, it is necessary that the inequality
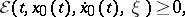 |
where 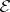 is the Weierstrass
is the Weierstrass 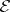 -function, be satisfied for all
-function, be satisfied for all  ,
, 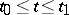 , and all
, and all 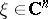 . This condition may be expressed in terms of the function
. This condition may be expressed in terms of the function
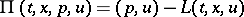 |
(cf. Pontryagin maximum principle). The Weierstrass condition (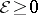 on the extremal
on the extremal 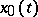 ) is equivalent to saying that the function
) is equivalent to saying that the function 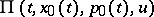 , where
, where 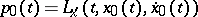 , attains a maximum in
, attains a maximum in  for
for 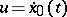 . Thus, Weierstrass' necessary condition is a special case of the Pontryagin maximum principle.
. Thus, Weierstrass' necessary condition is a special case of the Pontryagin maximum principle.
Weierstrass' sufficient condition: For the functional
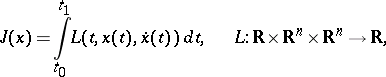 |
to attain a strong local minimum on the vector function 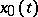 , it is sufficient that there exists a vector-valued field slope function
, it is sufficient that there exists a vector-valued field slope function 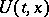 (geodesic slope) (cf. Hilbert invariant integral) in a neighbourhood
(geodesic slope) (cf. Hilbert invariant integral) in a neighbourhood 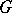 of the curve
of the curve 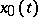 , for which
, for which
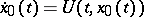 |
and
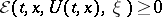 |
for all 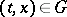 and any vector
and any vector 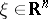 .
.
References
| [1] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
| [2] | G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947) |
| [3] | L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian) |
Comments
See also Weierstrass–Erdmann corner conditions, for necessary conditions at a corner of an extremal.
References
| [a1] | I.M. Gel'fand, S.V. Fomin, "Calculus of variations" , Prentice-Hall (1963) (Translated from Russian) |
| [a2] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
Weierstrass conditions (for a variational extremum). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_conditions_(for_a_variational_extremum)&oldid=17563