Weierstrass E-function
in the classical calculus of variations
A function which isolates the main part of the increment of a functional as the extremal is varied, using a local (needle-shaped) variation for a given value of its derivative, at a given point of the extremal. In the case of the functional
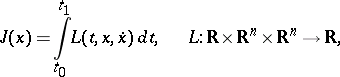 |
the 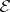 -function has the form
-function has the form
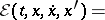 | (1) |
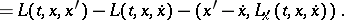 |
If one introduces the function
 |
(cf. Legendre transform; Pontryagin maximum principle), the 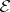 -function assumes the form
-function assumes the form
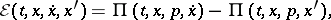 |
where 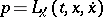 . The general construction of functions analogous to the
. The general construction of functions analogous to the  -function (1) consists of the following. Let
-function (1) consists of the following. Let 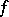 be a differentiable or convex function, defined on a Banach space
be a differentiable or convex function, defined on a Banach space 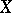 , and let
, and let 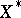 be the dual space. If the function
be the dual space. If the function  is defined by the equation
is defined by the equation
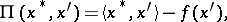 |
where 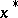 is the derivative
is the derivative 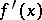 of
of 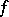 at
at  (or the subdifferential element if
(or the subdifferential element if 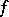 is convex), the function
is convex), the function
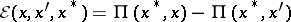 |
is the 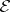 -function constructed from
-function constructed from 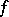 . If
. If 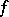 is differentiable,
is differentiable,
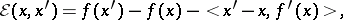 | (2) |
i.e. the 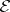 -function is the difference at
-function is the difference at 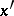 between
between 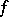 and the linear function tangent to
and the linear function tangent to 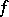 at
at  . A comparison of formulas (1) and (2) shows that in the classical calculus of variations the
. A comparison of formulas (1) and (2) shows that in the classical calculus of variations the 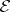 -function is obtained from the construction (2) with respect to the variables related to derivatives, while the variables
-function is obtained from the construction (2) with respect to the variables related to derivatives, while the variables 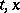 play the role of parameters.
play the role of parameters.
In the case of a functional
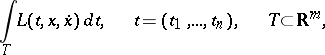 |
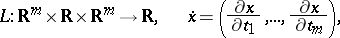 |
in a multi-dimensional variational problem, the 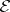 -function has the following form:
-function has the following form:
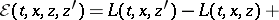 |
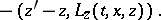 |
In the case of the Lagrange problem with boundaries 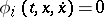 and Lagrange multipliers
and Lagrange multipliers 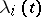 ,
, 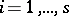 , the
, the 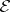 -function has the form (1), in which
-function has the form (1), in which
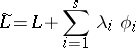 |
has been substituted for 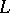 .
.
The 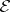 -function, first introduced in 1879 by K. Weierstrass [1], lies at the foundation of the theory of the calculus of variations (cf. Variational calculus). It is used in the formulation of necessary and (partially) sufficient conditions for an extremum (cf. Weierstrass conditions (for a variational extremum)), and serves to express the increment of a functional
-function, first introduced in 1879 by K. Weierstrass [1], lies at the foundation of the theory of the calculus of variations (cf. Variational calculus). It is used in the formulation of necessary and (partially) sufficient conditions for an extremum (cf. Weierstrass conditions (for a variational extremum)), and serves to express the increment of a functional 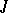 on an extremal in the form of a finite integral (cf. Weierstrass formula).
on an extremal in the form of a finite integral (cf. Weierstrass formula).
An especially important role in variational calculus is played by smooth functionals in which, in a given parameter range, 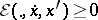 for all
for all 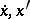 , or, stronger, if
, or, stronger, if 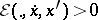 for all
for all  . They are known as quasi-regular and regular or elliptic, respectively. For such functionals the Legendre condition and the necessary Weierstrass conditions (for a variational extremum) are invariably valid, as are the theorems of existence and regularity [7].
. They are known as quasi-regular and regular or elliptic, respectively. For such functionals the Legendre condition and the necessary Weierstrass conditions (for a variational extremum) are invariably valid, as are the theorems of existence and regularity [7].
References
| [1] | K. Weierstrass, "Vorlesungen über Variationsrechnung" , Math. Werke , 7 , Akademie Verlag (1927) |
| [2] | C. Carathéodory, "Calculus of variations and partial differential equations of the first order" , 1–2 , Holden-Day (1965–1967) (Translated from German) |
| [3] | O. Bolza, "Lectures on the calculus of variations" , Chelsea, reprint (1960) (Translated from German) |
| [4] | N.I. Akhiezer, "The calculus of variations" , Blaisdell (1962) (Translated from Russian) |
| [5] | L.S. Pontryagin, V.G. Boltayanskii, R.V. Gamkrelidze, E.F. Mishchenko, "The mathematical theory of optimal processes" , Wiley (1962) (Translated from Russian) |
| [6] | M.R. Hestenes, "Calculus of variations and optimal control theory" , Wiley (1966) |
| [7] | "Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [8] | G.A. Bliss, "Lectures on the calculus of variations" , Chicago Univ. Press (1947) |
Comments
References
| [a1] | L. Cesari, "Optimization - Theory and applications" , Springer (1983) |
| [a2] | G.M. Ewing, "Calculus of variations with applications" , Dover, reprint (1985) |
| [a3] | E.B. Lee, L. Marcus, "Foundations of optimal control theory" , Wiley (1967) |
Weierstrass E-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_E-function&oldid=19110