Weak convergence of probability measures
The general setting for weak convergence of probability measures is that of a complete separable metric space  (cf. also Complete space; Separable space),
(cf. also Complete space; Separable space),  being the metric, with probability measures
being the metric, with probability measures  ,
,  defined on the Borel sets of
defined on the Borel sets of 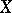 . It is said that
. It is said that  converges weakly to
converges weakly to  in
in  if for every bounded continuous function
if for every bounded continuous function  on
on 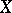 one has
one has 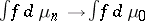 as
as 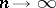 . If random elements
. If random elements 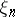 ,
, 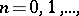 taking values in
taking values in 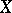 are such that the distribution of
are such that the distribution of 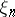 is
is 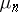 ,
,  one writes
one writes 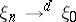 , and says that
, and says that 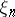 converges in distribution to
converges in distribution to 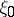 if
if 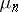 converges weakly to
converges weakly to 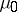 (cf. also Convergence in distribution).
(cf. also Convergence in distribution).
The metric spaces in most common use in probability are 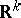 ,
, 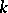 -dimensional Euclidean space,
-dimensional Euclidean space,  , the space of continuous functions on
, the space of continuous functions on 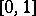 , and
, and 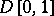 , the space of functions on
, the space of functions on 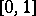 which are right continuous with left-hand limits.
which are right continuous with left-hand limits.
Weak convergence in a suitably rich metric space is of considerably greater use than that in Euclidean space. This is because a wide variety of results on convergence in distribution on 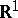 can be derived from it with the aid of the continuous mapping theorem, which states that if
can be derived from it with the aid of the continuous mapping theorem, which states that if 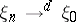 in
in 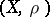 and the mapping
and the mapping 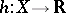 is continuous (or at least is measurable and
is continuous (or at least is measurable and 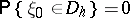 , where
, where 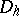 is the set of discontinuities of
is the set of discontinuities of 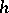 ), then
), then 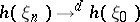 . In many applications the limit random element is Brownian motion, which has continuous paths with probability one.
. In many applications the limit random element is Brownian motion, which has continuous paths with probability one.
One of the most fundamental weak convergence results is Donsker's theorem for sums 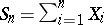 ,
, 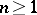 , of independent and identically-distributed random variables
, of independent and identically-distributed random variables 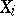 with
with  ,
, 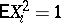 . This can be framed in
. This can be framed in 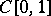 by setting
by setting  and
and 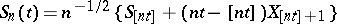 ,
, 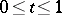 , where
, where 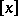 denotes the integer part of
denotes the integer part of  . Then Donsker's theorem asserts that
. Then Donsker's theorem asserts that 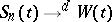 , where
, where 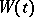 is standard Brownian motion. Application of the continuous mapping theorem then readily provides convergence-in-distribution results for functionals such as
is standard Brownian motion. Application of the continuous mapping theorem then readily provides convergence-in-distribution results for functionals such as 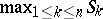 ,
, 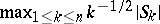 ,
, 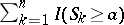 , and
, and 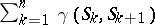 , where
, where 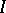 is the indicator function and
is the indicator function and 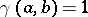 if
if 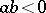 and
and  otherwise.
otherwise.
References
| [a1] | P. Billingsley, "Convergence of probability measures" , Wiley (1968) pp. 9ff |
Weak convergence of probability measures. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_convergence_of_probability_measures&oldid=16387