Voronoi lattice types

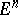Types of point lattices (cf. Lattice of points) in -dimensional Euclidean space , introduced in 1908 by G.F. Voronoi [1] in the context of a problem on parallelohedra.

A set of points in is called an 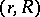-system if no point is closer to any other point than the given distance 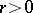, and if any sphere of radius larger than some given 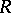contains at least one point of . Let 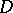be a convex polyhedron of the Dirichlet domain (or Dirichlet cell) of a point in , i.e. of the domain of points in space which are no more remote from that point than from all other points in the system. The Dirichlet domains of the points of an 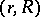-system have pairwise no common interior points, cover the entire space (i.e. form a partitioning) and have entire faces in common (i.e. constitute a normal partitioning). This system may be associated with another normal partitioning , dual to 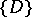, into polyhedra 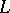(inscribed in spheres), each one of which is the convex envelope of the points of the system corresponding to all 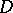which meet at a vertex of the partitioning .

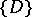Two -dimensional point lattices are of the same Voronoi type if their partitionings 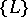are affine to each other. If a frame is such that, for sufficiently small changes of its metric parameters (of the scalar squares 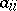and scalar products 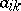(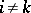) of its vectors), the partitioning of the lattice constructed on the modified frame is obtained from the partitioning 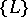of the lattice constructed on the initial frame by the same affine transformation which converts the initial into the modified frame, then the frame is called primitive or general. For this it is necessary and sufficient for the partitioning 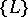of the initial frame to be simplicial. The point 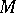of the space 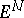of parameters 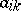, where 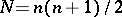, which corresponds to such a frame, is also known as general. A complete linearly connected domain 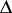, containing a general point, in which the partitionings 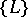for all its points are obtained from the partitioning 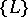for the lattice constructed on the frame corresponding to the point 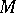by the same affine transformation which maps the initial frame into the frames corresponding to the other points is called the type domain of the point 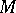. It was shown by Voronoi that the doma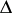in in 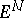has the form of a convex polyhedral angle (a gonohedron) with its vertex at the coordinate origin and with a finite number of faces, and that for any given there exist only a finite number 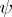of non-equivalent domains 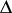. He also proposed an algorithm by which these could be found [1]. For 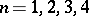the number 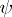is 1, 1, 1, 3, respectively. Voronoi also showed that the most general (i.e. not necessarily of Dirichlet type) normal partitioning of into identical convex, parallel polyhedra located such that 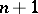meet at the vertices (primitive parallelohedra) is an affine image of the partitioning 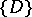for a lattice. Thus he reduced the study of such parallelohedra to the theory of quadratic forms. For non-primitive parallelohedra (i.e. more than 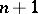parallelohedra meeting at certain vertices), the possibility of their affine transformation into the domain 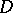of a lattice for arbitrary is still an open question. It is only known that a positive solution exists for .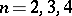

The primitive domain for a two-dimensional lattice is a convex hexagon with a centre of symmetry, inscribed in a circle, and vice versa. In the case of a three-dimensional lattice this is some 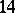-gon, which combinatorially resembles a cubo-octahedron with eight hexagonal and six tetragonal faces; each such face has a centre of symmetry such that the segments issuing from its centre into the centres of the faces are perpendicular to the faces and vice versa. The non-primitive domain 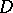for is a rectangle. For 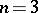it is either a dodecahedron with four hexagonal and eight parallelogrammatic faces, or a parallelogrammatic dodecahedron, or a vertical hexagonal prism with a primitive two-dimensional 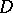as base, or a rectangular parallelepipedon. For 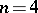there are three primitive 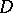of different Voronoi lattice types, as well as 49 non-primitive ones. The transition to 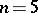is accompanied by a large jump — 221 different primitive [4]. This result was obtained by introducing the new concept of a 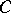-type lattice: Lattices with mutually affine one-dimensional skeletons of the partitioning 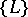rather than affine partitionings themselves, are said to have the same 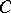-type.

References

[1]	G.F. Voronoi, "Studies of primitive parallelotopes" , Collected works , 2 , Kiev (1952) pp. 239–368 (In Russian)
[2a]	B.N. Delone, "Sur la partition reguliere de l'espace à quatre dimensions" Izv. Akad. Nauk SSSR Ser. 7, Otd. Fiz. Mat. Nauk : 1 (1929) pp. 79–110
[2b]	B.N. Delone, Izv. Akad. Nauk SSSR Ser. 7, Otd. Fiz. Mat. Nauk : 2 (1929) pp. 147–164
[3a]	B.N. Delone, "The geometry of positive quadratic forms" Uspekhi Mat. Nauk : 3 (1937) pp. 16–62 (In Russian)
[3b]	B.N. Delone, "The geometry of positive quadratic forms" Uspekhi Mat. Nauk : 4 (1938) pp. 102–164 (In Russian)
[4]	S.S. Ryshkov, E.P. Baranovskii, "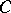-types of n-dimensional lattices and 5-dimensional primitive parellohedra (with an application to the theory of coverings)" Proc. Steklov Inst. Math. , 137 (1975) Trudy Mat. Inst. Steklov. , 137 (1975)

Comments

Instead of "Dirichlet cell" one also finds the phrases "Voronoi regionVoronoi region" , "first Brillouin zonefirst Brillouin zone" , "Dirichlet–Voronoi regionDirichlet–Voronoi region" "WabenzelleWabenzelle" , "honeycombhoneycomb" , "domain of actiondomain of action of z" . The partitioning or tiling by the Dirichlet–Voronoi regions is called "Dirichlet–Voronoi tilingDirichlet–Voronoi tiling" , "Dirichlet tilingDirichlet tiling" or "Voronoi tilingVoronoi tiling" . The Voronoi problem is whether each parallellohedron is the affine image of a Dirichlet–Voronoi region for a lattice. This is true for , [2a]. Cf. [a3], p. 170ff, for further results.

References

[a1]	J.H. Conway, N.J.A. Sloane, "Sphere packing, lattices and groups" , Springer (1988)
[a2]	P. Erdös, P.M. Gruber, J. Hammer, "Lattice points" , Longman (1989)
[a3]	P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) pp. Sect. (iv) (Updated reprint)
[a4]	B. Grünbaum, G.C. Shephard, "Tilings and patterns" , Freeman (1987)
[a5]	B.N. Delone, R.V. Galivlin, N.I. Shtogrin, "The types of Bravais lattices" J. Soviet Math. , 4 : 1 (1975) pp. 79–156 Sovrem. Probl. Mat. , 2 (1973) pp. 119–257