Vector bundle, analytic
A locally trivial analytic bundle over an analytic space whose fibres have the structure of an  -dimensional vector space over a ground field
-dimensional vector space over a ground field  (if
(if  is the field of complex numbers, the analytic bundle is said to be holomorphic). The number
is the field of complex numbers, the analytic bundle is said to be holomorphic). The number  is said to be the dimension, or rank, of the bundle. Similarly as for a topological bundle (cf. Vector bundle), definitions are given of the category of analytic vector bundles, and of the concepts of a subbundle, a quotient bundle, the direct sum, the tensor product, the exterior product of analytic vector bundles, etc.
is said to be the dimension, or rank, of the bundle. Similarly as for a topological bundle (cf. Vector bundle), definitions are given of the category of analytic vector bundles, and of the concepts of a subbundle, a quotient bundle, the direct sum, the tensor product, the exterior product of analytic vector bundles, etc.
The analytic sections of an analytic vector bundle with base  form a module
form a module  over the algebra
over the algebra  of analytic functions on the base. If
of analytic functions on the base. If  and
and  is compact,
is compact, 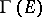 is a finite-dimensional vector space over
is a finite-dimensional vector space over 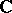 (see Finiteness theorems). If, on the other hand,
(see Finiteness theorems). If, on the other hand,  is a finite-dimensional complex Stein space, then
is a finite-dimensional complex Stein space, then  is a projective module of finite type over
is a projective module of finite type over  , and the correspondence
, and the correspondence 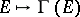 defines an equivalence between the category of analytic vector bundles over
defines an equivalence between the category of analytic vector bundles over  and the category of projective
and the category of projective 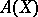 -modules of finite type [4].
-modules of finite type [4].
Examples of analytic vector bundles include the tangent bundle of an analytic manifold  (its analytic sections are analytic vector fields on
(its analytic sections are analytic vector fields on 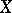 ), and the normal bundle of a submanifold
), and the normal bundle of a submanifold  .
.
The classification of analytic vector bundles of rank  on a given analytic space
on a given analytic space  is equivalent with the classification of principal analytic fibrations (cf. Principal analytic fibration) with base
is equivalent with the classification of principal analytic fibrations (cf. Principal analytic fibration) with base 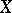 and structure group
and structure group  and, for
and, for  , has been completed only in certain special cases. For projective complex algebraic varieties
, has been completed only in certain special cases. For projective complex algebraic varieties 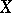 it is identical with the classification of algebraic vector bundles (cf. Comparison theorem (algebraic geometry)).
it is identical with the classification of algebraic vector bundles (cf. Comparison theorem (algebraic geometry)).
Analytic vector bundles of rank 1 on a complex space 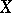 (in other words, bundles of complex lines, or line bundles) play an important part in complex analytic geometry. Each divisor on the space
(in other words, bundles of complex lines, or line bundles) play an important part in complex analytic geometry. Each divisor on the space 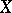 necessarily defines an analytic bundle of rank 1, two divisors defining isomorphic bundles if and only if they are linearly equivalent. All analytic line bundles on a projective algebraic variety are defined by a divisor. The imbeddability of a complex space
necessarily defines an analytic bundle of rank 1, two divisors defining isomorphic bundles if and only if they are linearly equivalent. All analytic line bundles on a projective algebraic variety are defined by a divisor. The imbeddability of a complex space 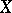 into a projective space is closely connected with the existence of ample line bundles on
into a projective space is closely connected with the existence of ample line bundles on 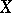 (cf. Ample vector bundle). If one is given a discrete group
(cf. Ample vector bundle). If one is given a discrete group  of automorphisms of a complex space
of automorphisms of a complex space 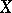 , each quotient of
, each quotient of 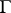 will determine a line bundle over
will determine a line bundle over 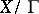 , with the respective automorphic forms as its analytic sections. Analytic vector bundles of rank 1 constitute the group
, with the respective automorphic forms as its analytic sections. Analytic vector bundles of rank 1 constitute the group 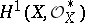 , where
, where  is the sheaf of invertible elements of the structure sheaf. The correspondence between each bundle and its first Chern class yields the homomorphism
is the sheaf of invertible elements of the structure sheaf. The correspondence between each bundle and its first Chern class yields the homomorphism
 |
whose kernel is the set of topologically trivial line bundles. If  is a complex manifold,
is a complex manifold,  may be described as the set of cohomology classes which are representable by closed differential forms of type
may be described as the set of cohomology classes which are representable by closed differential forms of type 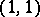 . If, in addition,
. If, in addition, 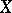 is compact and Kählerian,
is compact and Kählerian, 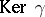 is isomorphic to the Picard variety of the manifold
is isomorphic to the Picard variety of the manifold  and is thus a complex torus [2].
and is thus a complex torus [2].
To each analytic vector bundle 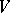 of rank
of rank  on an analytic space
on an analytic space  corresponds a sheaf of germs of analytic sections of
corresponds a sheaf of germs of analytic sections of  , which is a locally free analytic sheaf of rank
, which is a locally free analytic sheaf of rank  on
on 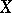 . This correspondence defines an equivalence between the categories of analytic vector bundles and locally free analytic sheaves on
. This correspondence defines an equivalence between the categories of analytic vector bundles and locally free analytic sheaves on 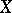 . Attempts to generalize this result to arbitrary coherent analytic sheaves resulted in the following generalization of the concept of an analytic vector bundle [3]: A surjective morphism
. Attempts to generalize this result to arbitrary coherent analytic sheaves resulted in the following generalization of the concept of an analytic vector bundle [3]: A surjective morphism  is said to be an analytic family of vector spaces over
is said to be an analytic family of vector spaces over 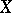 (or a linear space over
(or a linear space over  ) if its fibres have the structure of finite-dimensional vector spaces over
) if its fibres have the structure of finite-dimensional vector spaces over  , and if the operations of addition, multiplication by a scalar and the zero section satisfy the natural conditions of analyticity. If
, and if the operations of addition, multiplication by a scalar and the zero section satisfy the natural conditions of analyticity. If 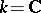 (or
(or  and
and  is coherent), the analytic family of vector spaces
is coherent), the analytic family of vector spaces  defines a coherent analytic sheaf
defines a coherent analytic sheaf 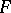 on
on 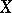 : For
: For 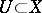 the group
the group  is the space of analytic functions on
is the space of analytic functions on 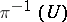 which are linear on the fibres. In the same way is defined the duality between the categories of analytic families of vector spaces and coherent analytic sheaves on
which are linear on the fibres. In the same way is defined the duality between the categories of analytic families of vector spaces and coherent analytic sheaves on 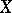 .
.
References
| [1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [2] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) |
| [3] | G. Fischer, "Lineare Faserräume und kohärente Modulgarben über komplexen Räumen" Arch. Math. (Basel) , 18 (1967) pp. 609–617 |
| [4] | O. Forster, K.J. Ramspott, "Über die Anzahl der Erzeugenden von projektiven Steinschen Moduln" Arch. Math. (Basel) , 19 (1968) pp. 417–422 |
Vector bundle, analytic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_bundle,_analytic&oldid=13046