Vaught conjecture
Let 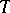 be a countable complete first-order theory (cf. also Logical calculus) and let
be a countable complete first-order theory (cf. also Logical calculus) and let 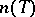 be the number of countable models of
be the number of countable models of 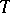 , up to isomorphism (cf. also Model theory);
, up to isomorphism (cf. also Model theory); 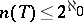 . In 1961, R. Vaught [a17] asked if one can prove, without using the continuum hypothesis CH, that there is some
. In 1961, R. Vaught [a17] asked if one can prove, without using the continuum hypothesis CH, that there is some 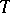 with
with 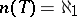 . Vaught's conjecture is the statement: If
. Vaught's conjecture is the statement: If 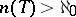 , then
, then 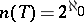 .
.
Variants of this conjecture have been formulated for incomplete theories, and for sentences in 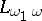 . In 1970, M. Morley [a10] proved, using descriptive set theory, that if
. In 1970, M. Morley [a10] proved, using descriptive set theory, that if 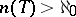 , then
, then 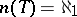 or
or 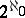 (actually, he proved this for any
(actually, he proved this for any 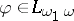 ).
).
Let 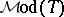 be the set of all models of
be the set of all models of 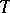 having
having 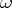 as their universe (cf. also Model theory). Morley equipped
as their universe (cf. also Model theory). Morley equipped 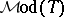 with a Polish topology (cf. also Descriptive set theory). Associated with each
with a Polish topology (cf. also Descriptive set theory). Associated with each 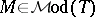 is a countable ordinal number,
is a countable ordinal number, 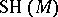 , called the Scott height (or Scott rank) of
, called the Scott height (or Scott rank) of 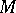 . Let
. Let 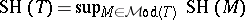 and, for
and, for 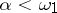 , let
, let 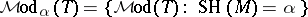 . The isomorphism relation
. The isomorphism relation 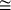 is analytic (
is analytic (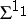 ; cf. also Luzin set) on
; cf. also Luzin set) on 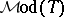 ; however,
; however, 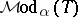 is Borel (cf. also Borel system of sets) and
is Borel (cf. also Borel system of sets) and 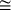 restricted to
restricted to 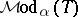 is a Borel equivalence relation, so
is a Borel equivalence relation, so 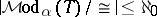 or
or 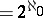 . Hence (if CH fails) the only possibility for
. Hence (if CH fails) the only possibility for 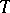 to have
to have 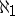 countable models is that
countable models is that 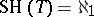 and for each
and for each 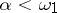 ,
, 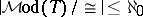 .
.
So the Vaught conjecture may be restated as follows: If 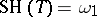 , then for some
, then for some 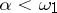 ,
, 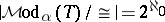 . This formulation does not depend explicitly on CH.
. This formulation does not depend explicitly on CH.
The above Morley analysis led to the so-called topological Vaught conjecture, which is a question regarding the number of orbits of a Polish topological group (cf. also Topological group) 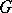 acting in a Borel way on a Polish space
acting in a Borel way on a Polish space 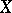 [a1], [a6].
[a1], [a6].
Vaught's conjecture was proved for theories of trees [a16], unary function [a7], [a9], varieties [a5], o-minimal theories [a8], and theories of modules over certain rings [a14].
In stable model theory, the combinatorial tools (like forking, cf. also Forking) developed by S. Shelah in [a4] enabled him to prove the Vaught conjecture for 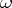 -stable theories [a15], which are at the lowest level of the stability hierarchy. Regarding superstable theories (the next level of the hierarchy), Vaught's conjecture was proved for weakly minimal theories [a3], [a11], and then for superstable theories of finite
-stable theories [a15], which are at the lowest level of the stability hierarchy. Regarding superstable theories (the next level of the hierarchy), Vaught's conjecture was proved for weakly minimal theories [a3], [a11], and then for superstable theories of finite 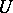 -rank [a2] and in some other cases [a12]. The proofs in these cases use advanced geometric properties of forking [a13].
-rank [a2] and in some other cases [a12]. The proofs in these cases use advanced geometric properties of forking [a13].
References
| [a1] | H. Becker, "The topological Vaught's conjecture and minimal counterexamples" J. Symbolic Logic , 59 (1994) pp. 757–784 |
| [a2] | S. Buechler, "Vaught's conjecture for superstable theories of finite rank" Ann. Pure Appl. Logic (to appear},) |
| [a3] | S. Buechler, "Classification of small weakly minimal sets, I" J.T. Baldwin (ed.) , Classification Theory, Proceedings, Chicago, 1985 , Springer (1987) pp. 32–71 |
| [a4] | S. Shelah, "Classification theory" , North-Holland (1990) (Edition: Second) |
| [a5] | B. Hart, S. Starchenko, M. Valeriote, "Vaught's conjecture for varieties" Trans. Amer. Math. Soc. , 342 (1994) pp. 173–196 |
| [a6] | G. Hjorth, G. Solecki, "Vaught's conjecture and the Glimm–Effros property for Polish transformation groups" Trans. Amer. Math. Soc. , 351 (1999) pp. 2623–2641 |
| [a7] | L. Marcus, "The number of countable models of a theory of unary function" Fundam. Math. , 108 (1980) pp. 171–181 |
| [a8] | L. Mayer, "Vaught's conjecture for o-minimal theories" J. Symbolic Logic , 53 (1988) pp. 146–159 |
| [a9] | A. Miller, "Vaught's conjecture for theories of one unary operation" Fundam. Math. , 111 (1981) pp. 135–141 |
| [a10] | M. Morley, "The number of countable models" J. Symbolic Logic , 35 (1970) pp. 14–18 |
| [a11] | L. Newelski, "A proof of Saffe's conjecture" Fundam. Math. , 134 (1990) pp. 143–155 |
| [a12] | L. Newelski, "Vaught's conjecture for some meager groups" Israel J. Math. , 112 (1999) pp. 271–299 |
| [a13] | L. Newelski, "Meager forking and 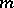 -independence" Documenta Math. , Extra ICM (1998) pp. 33–42 -independence" Documenta Math. , Extra ICM (1998) pp. 33–42 |
| [a14] | V. Puninskaya, "Vaught's conjecture for modules over a Dedekind prime ring" Bull. London Math. Soc. , 31 (1999) pp. 129–135 |
| [a15] | S. Shelah, L. Harrington, M. Makkai, "A proof of Vaught's conjecture for 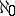 -stable theories" Israel J. Math. , 49 (1984) pp. 259–278 -stable theories" Israel J. Math. , 49 (1984) pp. 259–278 |
| [a16] | J. Steel, "On Vaught's conjecture" A. Kechris, Y. Moschovakis (ed.) , Cabal Seminar '76-77 , Lecture Notes in Mathematics , 689 , Springer (1978) pp. 193–208 |
| [a17] | R. Vaught, "Denumerable models of complete theories" , Infinitistic Methods (Proc. Symp. Foundations Math., Warsaw, 1959) , Państwowe Wydawnictwo Nauk. Warsaw/Pergamon Press (1961) pp. 303–321 |
Vaught conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vaught_conjecture&oldid=18041