Variety in a category
A notion generalizing that of a variety of universal algebras. Let  be a bicategory with products. A full subcategory
be a bicategory with products. A full subcategory  of
of  is called a variety if it satisfies the following conditions: a) if
is called a variety if it satisfies the following conditions: a) if  is an admissible monomorphism and
is an admissible monomorphism and  , then
, then  ; b) if
; b) if  is an admissible epimorphism and
is an admissible epimorphism and  , then
, then  ; c) if
; c) if 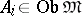 ,
,  , then
, then 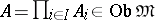 .
.
If 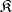 is well-powered, that is, the admissible subobjects of any object form a set, then every variety is a reflective subcategory of
is well-powered, that is, the admissible subobjects of any object form a set, then every variety is a reflective subcategory of 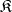 . This means that the inclusion functor
. This means that the inclusion functor  has a left adjoint
has a left adjoint  . The unit of this adjunction, the natural transformation
. The unit of this adjunction, the natural transformation  , has the property that for each
, has the property that for each 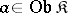 the morphism
the morphism 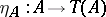 is an admissible epimorphism. In many important cases the functor
is an admissible epimorphism. In many important cases the functor 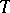 turns out to be right-exact, that is, it transforms the cokernel
turns out to be right-exact, that is, it transforms the cokernel  of a pair of morphisms
of a pair of morphisms 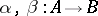 into the cokernel of the pair of morphisms
into the cokernel of the pair of morphisms 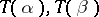 , if
, if 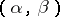 is a kernel pair of the morphism
is a kernel pair of the morphism  . Moreover, right exactness and the presence of the natural transformation
. Moreover, right exactness and the presence of the natural transformation 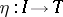 are characteristic properties of
are characteristic properties of 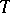 .
.
A variety inherits many properties of the ambient category. It has the structure of a bicategory, and is complete if the initial category is complete.
In categories with normal co-images, as in the case of varieties of groups, it is possible to define a product of varieties. The structure of the resultant groupoid of varieties has been studied only in a number of special cases.
References
| [1] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
| [2] | A. Fröhlich, "On groups over a d.g. near ring II. Categories and functors" Quart. J. Math. , 11 (1960) pp. 211–228 |
Comments
In a topos, one also considers exponential varieties [a1], which are full subcategories closed under arbitrary subobjects, products and power-objects. Such a subcategory is necessarily closed under quotients as well; it is a topos, and its inclusion functor has adjoints on both sides.
References
| [a1] | P.J. Freyd, "All topoi are localic, or why permutation models prevail" J. Pure Appl. Alg. , 46 (1987) pp. 49–58 |
Variety in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_in_a_category&oldid=11613