Difference between revisions of "User:Whayes43"
| Line 1: | Line 1: | ||
| − | + | ''for Euclidean geometry'' | |
| − | + | A system of axioms first proposed by D. Hilbert in 1899, and subsequently amended and made more precise by him.<ref>Hilbert (1899)</ref> | |
| − | + | In Hilbert's system of axioms the primary (primitive undefined) objects are $points$, (straight) $lines$, $planes$ and the relations between these terms are those of ''belonging to'', ''being between'', and ''being congruent to''. The nature of the primary objects and of the relations between those objects are arbitrary as long as the objects and the relations satisfy the axioms. | |
| − | |||
| − | |||
| − | + | Hilbert's system contains 20 axioms, which are subdivided into five groups. | |
| − | + | ===Group I: Axioms of Incidence or Connection=== | |
| + | This group comprises eight axioms which describe the relation ''belonging to''. | ||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474002.png" />. For any two points there exists a straight line passing through them. | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474003.png" />. There exists only one straight line passing through any two distinct points. | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474004.png" />. At least two points lie on any straight line. There exist at least three points not lying on the same straight line. | |
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474005.png" />. There exists a plane passing through any three points not lying on the same straight line. At least one point lies on any given plane. | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474006.png" />. There exists only one plane passing through any three points not lying on the same straight line. | |
| − | |||
| − | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474007.png" />. If two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474008.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h0474009.png" /> of a straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740010.png" /> lie in a plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740011.png" />, then all points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740012.png" /> lie in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740013.png" />. | ||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740014.png" />. If two planes have one point in common, then they have at least one more point in common. | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740015.png" />. There exist at least four points not lying in the same plane. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Group II: Axioms of Order=== | |
| + | This group comprises four axioms describing the relation ''being between''. | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740017.png" />. If a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740018.png" /> lies between a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740019.png" /> and a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740020.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740023.png" /> are distinct points on the same straight line and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740024.png" /> also lies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740025.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740026.png" />. | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740027.png" />. For any two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740028.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740029.png" /> on the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740030.png" /> there exists at least one point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740031.png" /> such that the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740032.png" /> lies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740033.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740034.png" />. | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740035.png" />. Out of any three points on the same straight line there exists not more than one point lying between the other two. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740036.png" /> (Pasch's axiom). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740038.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740039.png" /> be three points not lying on the same straight line, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740040.png" /> be a straight line in the plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740041.png" /> not passing through any of the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740042.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740043.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740044.png" />. Then, if the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740045.png" /> passes through an interior point of the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740046.png" />, it also passes through an interior point of the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740047.png" /> or through an interior point of the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740048.png" />. | |
| − | + | ===Group III: Axioms of Congruence=== | |
| + | This group comprises five axioms that describe the relation of "being congruent to" (Hilbert denoted this relation by the symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740050.png" />). | ||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740051.png" />. Given a segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740052.png" /> and a ray <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740053.png" />, there exists a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740054.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740055.png" /> such that the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740056.png" /> is congruent to the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740057.png" />, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740058.png" />. | |
| − | |||
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740059.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740060.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740061.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740062.png" />. | |
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740063.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740064.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740065.png" /> be two segments on a straight line without common interior points, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740066.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740067.png" /> be two segments on the same or on a different straight line, also without any common interior points. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740068.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740069.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740070.png" />. | |
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740071.png" />. Let there be given an angle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740072.png" />, a ray <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740073.png" /> and a half-plane <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740074.png" /> bounded by the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740075.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740076.png" /> contains one and only one ray <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740077.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740078.png" />. Moreover, every angle is congruent to itself. | |
| − | |||
| − | : | ||
| − | == | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740079.png" />. If for two triangles <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740080.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740081.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740082.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740083.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740084.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740085.png" />. |
| − | < | + | ===Group IV: Axioms of Continuity=== |
| + | This group comprises two continuity axioms. | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740087.png" /> (Archimedes' axiom). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740088.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740089.png" /> be two arbitrary segments. Then the straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740090.png" /> contains a finite set of points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740091.png" /> such that the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740092.png" /> lies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740093.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740094.png" />, the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740095.png" /> lies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740096.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740097.png" />, etc., and such that the segments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740098.png" /> are congruent to the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h04740099.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400100.png" /> lies between <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400101.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400102.png" />. | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400103.png" /> (Cantor's axiom). Let there be given, on any straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400104.png" />, an infinite sequence of segments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400105.png" /> which satisfies two conditions: a) each segment in the sequence forms a part of the segment which precedes it; b) for each preassigned segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400106.png" /> it is possible to find a natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400107.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400108.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400109.png" /> contains a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400110.png" /> belonging to all the segments of this sequence. | ||
| + | |||
| + | ===Group V: Axioms of Parallelism=== | ||
| + | This group comprises one axiom about parallels. | ||
| + | Let there be given a straight line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400112.png" /> and a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400113.png" /> not on that straight line. Then there exists not more than one straight line passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400114.png" />, not intersecting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400115.png" /> and lying in the plane defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400116.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400117.png" />. | ||
| + | |||
| + | (Hilbert classified the axiom about parallels in Group IV, and the continuity axioms in Group V). | ||
| + | |||
| + | All other axioms of Euclidean geometry are defined by the basic concepts of Hilbert's system of axioms, while all the statements regarding the properties of geometrical figures and not included in Hilbert's system must be logically deducible from the axioms, or from statements which are deducible from these axioms. | ||
| + | |||
| + | Hilbert's system of axioms is complete; it is consistent if the arithmetic of real numbers is consistent. If, in Hilbert's system, the axiom about parallels is replaced by its negation, the new system of axioms thus obtained is also consistent (the system of axioms of Lobachevskii geometry), which means that the axiom about parallels is independent of the other axioms in Hilbert's system. It is also possible to demonstrate that some other axioms of this system are independent of the others. | ||
| + | |||
| + | Hilbert's system of axioms was the first fairly rigorous foundation of [[Euclidean geometry|Euclidean geometry]]. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian)</TD></TR></table> | ||
| + | |||
| + | * Hilbert, D. (1899). "Grundlagen der Geometrie". [Reprint (1968) Teubner.] | ||
| + | * Efimov, N.V. (1960). "Höhere Geometrie", Deutsch. Verlag Wissenschaft. [Translated from Russian.] | ||
| + | |||
| + | |||
| + | ====Comments==== | ||
| + | In axiom <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400118.png" /> the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400119.png" /> is also called an interior point of the segment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047400/h047400120.png" /> (Pasch's axiom should be read with this in mind). | ||
| + | |||
| + | Also, Hilbert originally used different continuity axioms: the Archimedean axiom and a completeness axiom of his own. | ||
| + | |||
| + | ====References==== | ||
| + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H.G. Forder, "Foundations of Euclidean geometry" , Dover, reprint (1958)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.D. Aleksandrov, "Foundations of geometry" ''Siberian Math. J.'' , July 1987, Volume 28, Issue 4, pp 523-539'''28''' (1987) pp. 523–539 ''Sibirsk. Mat. Zh.'' , '''28''' (1987) pp. 9–28</TD></TR></table> | ||
| + | |||
| + | |||
| + | * Aleksandrov, A.D. "Foundations of geometry," ''Siberian Mathematical Journal'', July 1987, Vol. 28, Issue 4, pp 523-539. [Trans. ''Sibirskii Matematicheskii Zhurnal'', Vol. 28, No. 4, pp. 9–28, July–August, 1987.] | ||
| + | * Forder, H.G. "Foundations of Euclidean geometry". [Reprint (1958) Dover.] | ||
Revision as of 15:52, 16 September 2015
for Euclidean geometry
A system of axioms first proposed by D. Hilbert in 1899, and subsequently amended and made more precise by him.[1]
In Hilbert's system of axioms the primary (primitive undefined) objects are $points$, (straight) $lines$, $planes$ and the relations between these terms are those of belonging to, being between, and being congruent to. The nature of the primary objects and of the relations between those objects are arbitrary as long as the objects and the relations satisfy the axioms.
Hilbert's system contains 20 axioms, which are subdivided into five groups.
Group I: Axioms of Incidence or Connection
This group comprises eight axioms which describe the relation belonging to.
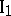 . For any two points there exists a straight line passing through them.
. For any two points there exists a straight line passing through them.
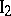 . There exists only one straight line passing through any two distinct points.
. There exists only one straight line passing through any two distinct points.
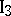 . At least two points lie on any straight line. There exist at least three points not lying on the same straight line.
. At least two points lie on any straight line. There exist at least three points not lying on the same straight line.
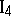 . There exists a plane passing through any three points not lying on the same straight line. At least one point lies on any given plane.
. There exists a plane passing through any three points not lying on the same straight line. At least one point lies on any given plane.
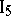 . There exists only one plane passing through any three points not lying on the same straight line.
. There exists only one plane passing through any three points not lying on the same straight line.
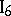 . If two points
. If two points 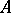 and
and 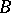 of a straight line
of a straight line  lie in a plane
lie in a plane  , then all points of
, then all points of  lie in
lie in 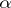 .
.
 . If two planes have one point in common, then they have at least one more point in common.
. If two planes have one point in common, then they have at least one more point in common.
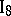 . There exist at least four points not lying in the same plane.
. There exist at least four points not lying in the same plane.
Group II: Axioms of Order
This group comprises four axioms describing the relation being between.
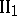 . If a point
. If a point 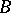 lies between a point
lies between a point 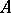 and a point
and a point  , then
, then 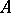 ,
, 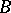 and
and 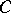 are distinct points on the same straight line and
are distinct points on the same straight line and 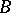 also lies between
also lies between 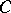 and
and 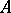 .
.
 . For any two points
. For any two points 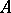 and
and 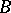 on the straight line
on the straight line 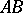 there exists at least one point
there exists at least one point 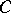 such that the point
such that the point 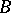 lies between
lies between 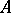 and
and  .
.
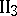 . Out of any three points on the same straight line there exists not more than one point lying between the other two.
. Out of any three points on the same straight line there exists not more than one point lying between the other two.
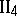 (Pasch's axiom). Let
(Pasch's axiom). Let 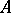 ,
, 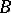 and
and 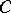 be three points not lying on the same straight line, and let
be three points not lying on the same straight line, and let  be a straight line in the plane
be a straight line in the plane 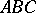 not passing through any of the points
not passing through any of the points  ,
,  or
or 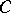 . Then, if the straight line
. Then, if the straight line  passes through an interior point of the segment
passes through an interior point of the segment 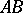 , it also passes through an interior point of the segment
, it also passes through an interior point of the segment 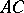 or through an interior point of the segment
or through an interior point of the segment  .
.
Group III: Axioms of Congruence
This group comprises five axioms that describe the relation of "being congruent to" (Hilbert denoted this relation by the symbol  ).
).
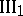 . Given a segment
. Given a segment 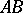 and a ray
and a ray  , there exists a point
, there exists a point 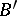 on
on 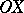 such that the segment
such that the segment 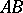 is congruent to the segment
is congruent to the segment 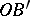 , i.e.
, i.e. 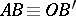 .
.
 . If
. If 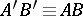 and
and 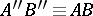 , then
, then 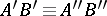 .
.
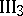 . Let
. Let 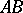 and
and 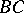 be two segments on a straight line without common interior points, and let
be two segments on a straight line without common interior points, and let 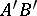 and
and 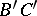 be two segments on the same or on a different straight line, also without any common interior points. If
be two segments on the same or on a different straight line, also without any common interior points. If 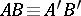 and
and 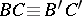 , then
, then 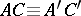 .
.
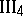 . Let there be given an angle
. Let there be given an angle 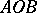 , a ray
, a ray 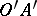 and a half-plane
and a half-plane 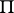 bounded by the straight line
bounded by the straight line 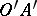 . Then
. Then 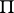 contains one and only one ray
contains one and only one ray 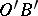 such that
such that 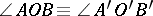 . Moreover, every angle is congruent to itself.
. Moreover, every angle is congruent to itself.
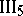 . If for two triangles
. If for two triangles  and
and 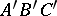 one has
one has 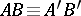 ,
, 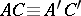 ,
, 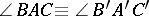 , then
, then 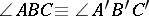 .
.
Group IV: Axioms of Continuity
This group comprises two continuity axioms.
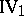 (Archimedes' axiom). Let
(Archimedes' axiom). Let 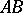 and
and 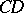 be two arbitrary segments. Then the straight line
be two arbitrary segments. Then the straight line 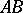 contains a finite set of points
contains a finite set of points 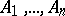 such that the point
such that the point 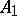 lies between
lies between 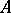 and
and 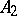 , the point
, the point 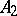 lies between
lies between 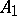 and
and 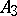 , etc., and such that the segments
, etc., and such that the segments 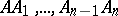 are congruent to the segment
are congruent to the segment  , and
, and 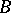 lies between
lies between 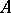 and
and 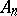 .
.
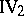 (Cantor's axiom). Let there be given, on any straight line
(Cantor's axiom). Let there be given, on any straight line  , an infinite sequence of segments
, an infinite sequence of segments 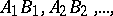 which satisfies two conditions: a) each segment in the sequence forms a part of the segment which precedes it; b) for each preassigned segment
which satisfies two conditions: a) each segment in the sequence forms a part of the segment which precedes it; b) for each preassigned segment 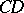 it is possible to find a natural number
it is possible to find a natural number  such that
such that 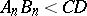 . Then
. Then  contains a point
contains a point 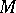 belonging to all the segments of this sequence.
belonging to all the segments of this sequence.
Group V: Axioms of Parallelism
This group comprises one axiom about parallels.
Let there be given a straight line  and a point
and a point 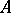 not on that straight line. Then there exists not more than one straight line passing through
not on that straight line. Then there exists not more than one straight line passing through 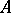 , not intersecting
, not intersecting  and lying in the plane defined by
and lying in the plane defined by  and
and 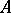 .
.
(Hilbert classified the axiom about parallels in Group IV, and the continuity axioms in Group V).
All other axioms of Euclidean geometry are defined by the basic concepts of Hilbert's system of axioms, while all the statements regarding the properties of geometrical figures and not included in Hilbert's system must be logically deducible from the axioms, or from statements which are deducible from these axioms.
Hilbert's system of axioms is complete; it is consistent if the arithmetic of real numbers is consistent. If, in Hilbert's system, the axiom about parallels is replaced by its negation, the new system of axioms thus obtained is also consistent (the system of axioms of Lobachevskii geometry), which means that the axiom about parallels is independent of the other axioms in Hilbert's system. It is also possible to demonstrate that some other axioms of this system are independent of the others.
Hilbert's system of axioms was the first fairly rigorous foundation of Euclidean geometry.
References
| [1] | D. Hilbert, "Grundlagen der Geometrie" , Teubner, reprint (1968) |
| [2] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
- Hilbert, D. (1899). "Grundlagen der Geometrie". [Reprint (1968) Teubner.]
- Efimov, N.V. (1960). "Höhere Geometrie", Deutsch. Verlag Wissenschaft. [Translated from Russian.]
Comments
In axiom 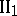 the point
the point 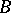 is also called an interior point of the segment
is also called an interior point of the segment 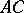 (Pasch's axiom should be read with this in mind).
(Pasch's axiom should be read with this in mind).
Also, Hilbert originally used different continuity axioms: the Archimedean axiom and a completeness axiom of his own.
References
| [a1] | H.G. Forder, "Foundations of Euclidean geometry" , Dover, reprint (1958) |
| [a2] | A.D. Aleksandrov, "Foundations of geometry" Siberian Math. J. , July 1987, Volume 28, Issue 4, pp 523-53928 (1987) pp. 523–539 Sibirsk. Mat. Zh. , 28 (1987) pp. 9–28 |
- Aleksandrov, A.D. "Foundations of geometry," Siberian Mathematical Journal, July 1987, Vol. 28, Issue 4, pp 523-539. [Trans. Sibirskii Matematicheskii Zhurnal, Vol. 28, No. 4, pp. 9–28, July–August, 1987.]
- Forder, H.G. "Foundations of Euclidean geometry". [Reprint (1958) Dover.]
Whayes43. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Whayes43&oldid=36714